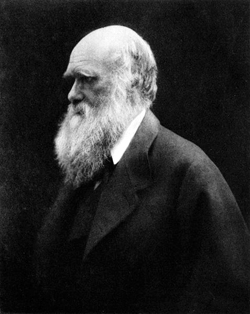Ciencia – Página 51

La fotógrafa de Darwin

9 septiembre 20098 septiembre 2010 Almudena M. Castro2 comentarios

477px-Charles_Darwin_by_Julia_Margaret_Cameron_2 Este es, probablemente, uno de los mejores retratos que hoy conservamos de Charles Darwin. Frente a la fotografía tomada en 1881 por Herbert Rose Barraud, esta imagen presenta todavía a un Darwin saludable, aparentemente absorto en sus pensamientos, imponente y lúcido.

Tirando del hilo de la curiosidad, me enteré de que este retrato fue tomado en 1868 por una de las mejores fotógrafas del siglo XIX: Julia Margaret Cameron, aunque esta no es probablemente su mejor obra. Cameron relizó una gran cantidad de retratos y fotografías alegóricas que sorprenden por su moderno lenguaje y plantemiento, sobre todo si los comparamos con los de otros fotógrafos del siglo XIX. De hecho, la obra de esta artista fue más reconocida de forma póstuma. En vida, en cambio, muchos reprochaban las imperfecciones técnicas de su trabajo. Fue una de las primeras en considerar la fotografía como un medio de creación artística, más que un mero registro de la realidad (planteamiento que reivindicarían más tarde los fotógrafos pictorialistas). Probablemente por ello, provocaba ciertos desenfoques y anomalías en sus imágenes que les daban ese aire romático característico, pero que le valieron también la dura crítica de sus contemporáneos. Desenfocadas o no, algunas de sus fotografías son sencillamente geniales.

Cameron-Beatrice — Detalles de distintas fotos alegóricas de Julia Margaret Cameron.

julia-margaret-cameron — Detalles de distintas fotos alegóricas de Julia Margaret Cameron.

558px-Sir_John_Herschel_with_Cap_by_Julia_Margaret_Cameron_(detail) — Retratos de personajes del siglo XIX: John Herschel, científico inglés, Ellen Terry, actriz y Julia Jackson, sobrina de Cameron.

Ellen_Terry_at_age_16_by_Julia_Margaret_Cameron — Retratos de personajes del siglo XIX: John Herschel, científico inglés, Ellen Terry, actriz y Julia Jackson, sobrina de Cameron.

Gracias a su posición social elevada, Cameron estuvo en contacto con los grandes literatos, artistas y científicos de la sociedad inglesa de su época y realizó retratos de muchos ellos (en su casa habilitó un gallinero como estudio fotográfico). Conoció a Darwin gracias a un amigo común, el poeta Alfred Tennyson. En 1868 el científico encargaría la primera sesión de fotos a Cameron, a la que correponden algunas de sus imágenes más conocidas y entre ellas, la que hoy os presento.

Tirando aún más del hilo, averigüé que Lewis Carroll fue quien instruyó a Cameron en la técnica fotográfica. Sí, el autor de Alicia en el país de las maravillas fue también un pionero de la fotografía. Pero no sería el único literato en la vida de Cameron. Una de sus modelos más recurrentes era su sobrina Julia Jackson. Ella no escribió nada, pero su hija, (activa reivindicadora de la fotografía de su tía Cameron) fue Virginia Woolf, la genial escritora en la que está inspirada la película Las Horas y que yo os recomiendo leer encarecidamente (sobre su novela Orlando).

Primera imagen de una molécula de pentaceno

30 agosto 20098 septiembre 2010 Almudena M. Castro8 comentarios

Leo en EL PAÍS que científicos del laboratorio de IBM en Zúrich han conseguido, por primera vez, una imagen de una molécula de pentaceno, de 1,4 nanómetros de longitud, a través de un microscopio de fuerza atómica (o AFM, Atomic Force Microscope). Desconozco el alcance de este logro: al parecer, tiene una gran relevancia de cara al desarrollo de la nanotecnología. Pero a mí, lo que verdaderamente me llama la atención es lo mucho que se parece la molécula a cómo lo habíamos imaginado.

20090828elpepusoc_8 — Estructura interna de una molécula de pentaceno (C22H14). Abajo, modelo de la misma (los átomos grises son de carbono y los blancos de hidrógeno).

A ciertas escalas, la ciencia no deja de tener cierto carácter fantástico: debemos imaginar que los átomos están ahí y son de tal manera, aunque no podamos verlos, tocarlos u oírlos. Por eso, resulta tan impactante poder VER lo que hasta ahora no era más que una narración teórica, el gráfico del libro de química del colegio, y comprobar así que la teoría, de hecho, funciona.

Más impactante es aún el funcionamiento del AFM. Este artilugio consta de una varilla microscópica acabada en una finísima punta. Esta sirve para recorrer la muestra, explorando su topografía (algo así como la punta de un gramófono). Mediante un láser y un fotodetector se mide hasta la más mínima variación de la varilla y así se obtiene la imagen. Lo más impresionante es que, evidentemente, para medir una muestra del tamaño de una molécula, la punta de la varilla, tiene que ser menor que dicha muestra y poder acercarse lo suficiente (menos de 1 nm), sin reaccionar con ella. Los científicos de Zúrich probaron con distintos materiales (la mayoría de los cuales se pegaban a la muestra), hasta concluir que aquello que les daba mejor resolución y contraste, era una punta acabada en una molécula de monóxido de carbono. Cuando esta punta se aproxima a los átomos que forman el pentaceno o sus enlaces, experimenta una fuerza de repulsión, sin que llegue a haber contacto físico entre ambas (de hecho, el microscopio se denomina también NC-AFM, Noncontact-AFM). Esto se debe al principio de exclusión de Pauli, según el cual, las moléculas no pueden aproximarse arbitrariamente entre sí, porque sus respectivos electrones no pueden entrar en el mismo estado.

Ciencia y arte. Macoto Murayama

13 agosto 20098 septiembre 2010 Almudena M. Castro

Me ha encandilado el trabajo de Macoto Murayama, que descubro a través de haha.nu. Este artista japonés representa distintos tipos de flores, realzando su estructura geométrica: flora inorgánica, lleva por título. Se trata pues de una interpretación idealizada de un elemento de la naturaleza, que nos permite comprender mejor su estructura, resultando (¿por ello?) increíblemente estética. ¿No se parece en parte, a lo que persigue la ciencia? A mí al menos, estas imágenes me recuerdan a las ilustraciones de los antiguos naturalistas, realizadas con más medios, eso sí.

murayama_14 — Lily: Ambas imágenes corresponden a un lirio o azucena.

murayama_13 — Lily: Ambas imágenes corresponden a un lirio o azucena.

Música y matemáticas. La afinación temperada

12 agosto 20098 junio 2014 Almudena M. Castro38 comentarios

A pesar de que el sistema de afinación pitagórico es el único que respecta las dos consonancias principales (8^as y 5^as), la incompatibilidad entre ambas daba lugar a bastantes inconvenientes, tal como vimos la semana pasada. Como alternativa se propusieron otros sistemas a lo largo de la historia, algunos basados en la consonancia de 3ª (como el sistema justo o el mesotónico), otros, en unidades interválicas más pequeñas que el semitono (sistema de Holder, por ejemplo). No tengo especial interés en estos sistemas, pues creo que no aportaron mucho al sistema actual, pero se puede hablar de ellos en otra entrada si alguien tiene interés. Finalmente, el sistema que se impuso fue el sistema temperado, o temperamento igual (en inglés Equal Temperament, ET), basado en 12 semitonos iguales y que sólo respeta la consonancia de 8ª. Todas los demás intervalos, como veremos en esta entrada, resultan ligeramente disonantes. A pesar de ello, es un sistema óptimo para la música tonal, especialmente a partir del Barroco y el Clasicismo: cada vez más llena de modulaciones (cambios de tonalidad o de «escala»), alteraciones accidentales, cromatismos (empleo consecutivo de intervalos de semitono), etcétera.

El semitono temperado:

Es fácil deducir la razón de ser matemática del sistema temperado. Para ello intentaremos averiguar cuánto mide el intervalo de semitono en este sistema. Un intervalo es una proporción de frecuencias, por lo que la frecuencia de cada nota de la escala cromática, se obtendrá de multiplicar la nota anterior por la proporción (razón) correspondiente a un semitono, que por el momento llamaremos «x». Si queremos saber, por ejemplo, cuál es la frecuencia de do#, multiplicaremos la frecuencia de do por «x». Para obtener re, volveremos a multiplicar el resultado obtenido por x, (o la frecuencia de do por x²), etcétera. Por tanto, si queremos completar una 8ª con 12 intervalos iguales, necesitamos un semitono tal que al multiplicarlo 12 veces consecutivas por la frecuencia base, (pongamos 1), dé como resultado una frecuencia doble, (2, el mismo sonido una 8ª más agudo). Esto es: $1 \cdot x^ {12} = 2$ . Por tanto, $x = \sqrt[12] {2} = 1,059$ . Esta es la relación de frecuencias correspondiente a un semitono temperado. Este semitono es intermedio de los pitagóricos: diatónico, $256 / 243 = 1,053$ , y cromático, $2187 / 2048 = 1,068$ .

La escala temperada:

Para hallar la proporción correspondiente a cualquier otro intervalo de la escala temperada, tan sólo tendremos que elevar $\sqrt[12] {2}$ al número de semitonos (ST) que contiene dicho intervalo. En la tabla podéis ver una comparativa entre los intervalos pitagóricos, los temperados y los consonantes. Algunas consonancias están entre paréntesis porque son resultado de la inversión de otro intervalo consonante: la 4ªJ es una inversión de la 5ªJ (de do a sol hay una 5ªJ, de sol al do más agudo hay una 4ª), la 3ªm es el intervalo que hay entre mi y sol, ambos consonancias de do, por lo que también suele considerarse consonante, por último, la 6ªM es la inversión de la 3ªm.

Nota

También podéis apreciar las diferencias de afinación en este gráfico extraído de la wikipedia, aunque con algunos errores corregidos del original. Los puntos negros son temperados y los azules pitagóricos. El cent es una medida de afinación equivalente a la centésima parte (logarítmica, claro está) de un semitono temperado: $1 cent = \sqrt[120] {2}$

ETvsPythagorean

Como podéis ver, ambos sistemas son muy parecidos. Las mayores diferencias se encuentran entre las notas alteradas, especialmente al llegar al sol# (extremo del círculo de 5^as). Sin embargo, si escuchamos la escala diatónica de los sonidos naturales, afinada según el sistema pitagórico o el temperado, resultan casi indistinguibles.

La 5ª Justa:

la 5ªJ temperada es casi idéntica a la pitagórica: difieren aproximadamente 2 cents. Para que os hagáis una idea, podéis escuchar cómo suenan dos sonidos que difieren en 1 cent, 6 ó 10 en esta página de la wikipedia. Son indistinguibles.

La diferencia entre ambas 5^as recibe el nombre de schisma. Para calcular cuánto mide basta dividir la 5ª pitagórica entre la temperada, o bien, repartir la coma pitagórica entre las 12 quintas que cierran el círculo en el sistema temperado. El resultado es el mismo: $\frac{3}{2} \div \sqrt[12] {2^7} = \sqrt[12]{\left( \frac{3}{2} \right)^{12} \div 2^7} = 1,00113$

La 3ª Mayor.

La 3ªM difiere algo más entre un sistema y otro, pero sigue siendo claramente disonante en ambos. Hasta no oírlo, yo no imaginaba cuanto, así que aquí tenéis el intervalo afinado en ambos sistemas y una 3ªM consonante para compararlos.