Hay un detalle que Eugenio, en todas sus argumentaciones contra la conspiración lunar, siempre ha pasado por alto. Si los Estados Unidos hubiesen llegado realmente a la Luna…
Categoría: Ciencia
Artículos de divulgación científica.
Ciencia y arte. El origen del cine
Debemos el nacimiento del cine a una duda absurda, de las que aparecen de repente a las 3 de la madrugada y permanecen en nuestra cabeza lo que tarda en vaciarse la cerveza. Pero, para variar, esta duda duró lo suficiente para dar sus frutos.
En 1872, dos grupos de aficionados a la hípica de California, discutían si, durante el galope de un caballo, había algún momento en el que sus cuatro patas permaneciesen en el aire, sin tocar el suelo. Para ello, encargaron a Eadweard Muybridge que tratara de captar con su cámara el movimiento de un caballo de carreras. Los primeros experimentos resultaron infructuosos, pero con el tiempo, Muybridge fue perfeccionando su técnica hasta lograr sincronizar varias cámaras con un sistema de disparo lo bastante rápido para captar una imagen nítida del animal. Su primera serie consta de 12 fotografías tomadas en 1878 y conocida más tarde como Caballo en movimiento (Horse in motion).
La duda estaba resuelta: el caballo llegaba a levantar todas sus patas a la vez, y ese mismo año la revista Scientific American publicó seis grabados hechos sobre negativos ampliados de fotografías de Muybridge. La ciencia tenía su trozo del pastel, pero el futuro cine acababa de ver nacer a sus abuelos. El resto de la descendencia os la podéis imaginar: primero pusieron estas imágenes a rodar en zoótropos o fenaquitiscopios, después al propio Muybridge se le ocurrió proyectar esas imágenes dando lugar al zoopraxiscopio. Otros inventores de la época se interesaron por el tema: Edison y Dickson presentaron su quinetoscopio en 1891. Pero no podemos hablar de «cine» hasta 1895, cuando los hermanos Lumière proyectaron públicamente la salida de obreros de una fábrica de Lyon, con su nuevo cinematógrafo.
La capacidad de percibir movimiento a partir de varias imágenes estáticas, también dice mucho sobre nuestro sistema perceptivo. Al principio se pensaba que era un fenómeno puramente óptico, que nuestro ojo era engañado por la «persistencia retiniana». Hoy pensamos que el fenómeno tiene lugar en el cerebro, encargado de interpretar las imágenes que recibe; unas 16 al segundo son suficientes para que veamos un movimiento continuo. Gracias a ello, podemos incluso simular movimiento donde nunca lo hubo, con técnicas de animación como el stop-motion, origen de todas las películas hechas con plastilina y de este magnífico video-clip, el verdadero culpable de que yo haya escrito este ladrillo.
Romance matemático
De algún número de 1990 de la revista de la Escuela de Ingenieros Industriales de Madrid. Visto en CienciaNet.
Veraneaba una derivada enésima en un pequeño chalet situado en la recta del infinito del plano de Gauss, cuando conoció a un arcotangente simpatiquísimo y de espléndida representación gráfica, que además pertenecía a una de las mejores familias trigonométricas.
En seguida notaron que tenían propiedades comunes.
Un día, en casa de una parábola que había ido a pasar allí una temporada con sus ramas alejadas, se encontraron en un punto aislado de ambiente muy íntimo. Se dieron cuenta de que convergían hacia límites cuya diferencia era tan pequeña como se quisiera. Había nacido un romance. Acaramelados en un entorno de radio épsilon, se dijeron mil teoremas de amor.
Cuando el verano pasó, y las parábolas habían vuelto al origen, la derivada y el arcotangente eran novios. Entonces empezaron los largos paseos por las asíntotas siempre unidos por un punto común, los interminables desarrollos en serie bajo los conoides llorones del lago, las innumerables sesiones de proyección ortogonal.
Hasta fueron al circo, donde vieron a una troupe de funciones logarítmicas dar saltos infinitos en sus discontinuidades. En fin, lo que eternamente hacían los novios.
Durante un baile organizado por unas cartesianas, primas del arcotangente, la pareja pudo tener el mismo radio de curvatura en varios puntos. Las series melódicas eran de ritmos uniformemente crecientes y la pareja giraba entrelazada alrededor de un mismo punto doble. Del amor había nacido la pasión. Enamorados locamente, sus gráficas coincidían en más y más puntos.
Con el beneficio de las ventas de unas fincas que tenía en el campo complejo, el arcotangente compró un recinto cerrado en el plano de Riemann. En la decoración se gastó hasta el último infinitésimo. Adornó las paredes con unas tablas de potencias de «e» preciosas, puso varios cuartos de divisiones del término independiente que costaron una burrada.
Empapeló las habitaciones con las gráficas de las funciones más conocidas, y puso varios paraboloides de revolución chinos de los que surgían desarrollos tangenciales en flor. Y Bernouilli le prestó su lemniscata para adornar su salón durante los primeros días. Cuando todo estuvo preparado, el arcotangente se trasladó al punto impropio y contempló satisfecho su dominio de existencia.
Varios días después fue en busca de la derivada de orden «n» y cuando llevaban un rato charlando de variables arbitrarias, le espetó, sin más:
—¿Por qué no vamos a tomar unos neperianos a mi apartamento? De paso lo conocerás, ha quedado monísimo.
Ella, que le quedaba muy poco para anularse, tras una breve discusión del resultado, aceptó.
El novio le enseñó su dominio y quedó integrada. Los neperianos y una música armónica simple, hicieron que entre sus puntos existiera una correspondencia unívoca. Unidos así, miraron al espacio euclídeo. Los astroides rutilaban en la bóveda de Viviany… ¡Eran felices!
—¿No sientes calor? —dijo ella.
—Yo si. ¿Y tú?
—Yo también.
—Ponte en forma canónica, estarás mas cómoda.
Entonces él le fue quitando constantes. Después de artificiosas operaciones la puso en paramétricas racionales…
—¿Que haces? Me da vergüenza… —dijo ella.
—¡Te amo, yo estoy inverso por ti!… ¡Déjame besarte la ordenada en el origen! ¡No seas cruel!… ¡ven! Dividamos por un momento la nomenclatura ordinaria y tendamos juntos hacia el infinito…
Él le acarició sus máximos y sus mínimos y ella se sintió descomponer en fracciones simples.
(Las siguientes operaciones quedan a la penetración del lector)
Al cabo de algún tiempo la derivada enésima perdió su periodicidad. Posteriores análisis algebraicos demostraron que su variable había quedado incrementada y su matriz era distinta de cero.
Ella le confesó a él, saliéndole los colores:
—Voy a ser primitiva de otra función.
Él respondió:
—Podríamos eliminar el parámetro elevando al cuadrado y restando.
—¡Eso es que ya no me quieres!
—No seas irracional, claro que te quiero. Nuestras ecuaciones formarán una superficie cerrada, confía en mí.
La boda se preparó en un tiempo diferencial de «t», para no dar que hablar en el círculo de los 9 puntos. Los padrinos fueron el padre de la novia, un polinomio lineal de exponente entero, y la madre del novio, una asiroide de noble asíntota. La novia lucía coordenadas cilíndricas de Satung y velo de puntos imaginarios. Ofició la ceremonia Cayley, auxiliado por Pascal y el nuncio S.S. monseñor Ricatti.
Hoy día el arcotangente tiene un buen puesto en una fábrica de series de Fourier, y ella cuida en casa de 5 lindos términos de menor grado, producto cartesiano de su amor.
Vocación musical

Si no fuese físico […], sería probablemente músico. Con frecuencia pienso en música. Vivo mis ensoñaciones en forma de música. Veo mi vida en términos de música. No sabría decirle si habría realizado algún trabajo creativo de importancia en el campo de la música, lo que sí sé es que lo que más placer me da en la vida es mi violín.
(Albert Einstein, físico alemán, en un libro de entrevistas titulado Glimpses of the Great, de 1930)
Cruzando los ojos
El hecho de tener dos ojos es el factor principal (aunque no el único) que influye en que percibamos el mundo con profundidad, en tres dimensiones. Cuando enfocamos un objeto, nuestros ojos, separados por unos 65 mm, tienen perspectivas ligeramente distintas. Después, nuestro cerebro es el encargado de fundir estas dos imágenes parecidas pero no iguales. Por eso, cuando observamos una imagen plana, una fotografía, por ejemplo, perdemos ese realismo, esa sensación de profundidad, porque los dos ojos llevan la misma información.
Existen diversas técnicas para producir este efecto sobre una imagen en 2D y que se basan en el mismo principio (mostrar una imagen ligeramente distinta a cada ojo), a saber:
- Método de anaglifo: consiste en dos imágenes filtradas por color y superpuestas. Se necesitan unas gafas especiales, con un cristal de cada color, para que, en cada lente, una imagen se cancele y la otra no.
- Método de lentes polarizadas: las dos imágenes también se superponen, pero cada una se emite con una polarización diferente (habitualmente una polarizada en vertical y la otra en horizontal). En cada ojo irá una lente con la polarización correspondiente, de forma que se filtra sólo una imagen.
- Método de imagen entrelazada: específico del vídeo en 3D. El entrelazado consiste en emitir alternativamente las líneas pares y las impares de las diapositivas de un vídeo para duplicar la velocidad aparente, puesto que el cerebro no se entera de esta treta. Si asignamos distinta perspectiva a las líneas pares con respecto a las impares, junto con unas gafas especiales, conseguimos el efecto de 3 dimensiones. En este caso, estas gafas son más caras, puesto que deben llevar un mecanismo que se cierre y se abra a la misma velocidad que pasan los frames (y en sincronía con ellos).
Sin embargo, hay un método más barato para crear la sensación de 3D, pero requiere poner un poco de nuestra parte. Veamos:
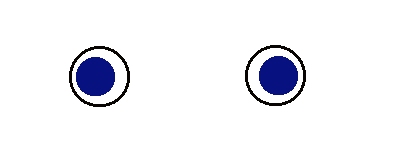
Yo digo que son dos imágenes de un punto azul que flota sobre una circunferencia, tomadas desde perspectivas diferentes, y vosotros hacéis un acto de fe, ¿de acuerdo? Bien. Ahora tenéis que verlo. Para ello:
- Colocad la cabeza a una distancia normal del ordenador, ni muy cerca ni muy lejos.
- Cruzad ligeramente los ojos (como si fuerais bizcos) hasta que veáis tres círculos borrosos.
- Obviad los dos de los lados y concentraos en el del centro, no lo perdáis. El objetivo es enfocarlo. Cuando lo consigáis, lo veréis en 3D.
Al principio cuesta, y hay que decir que no todo el mundo puede. Cuando se consigue, es una sensación impresionante. ¡Estamos engañando a nuestro cerebro! ¡Nos estamos engañando… ouch! Probad con esta niña, a mí me ha resultado más fácil:
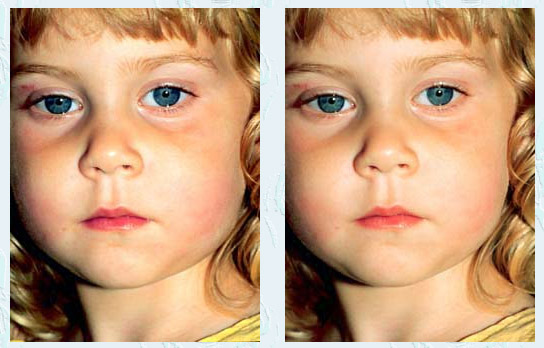
Si lo habéis conseguido, os habréis quedado con las ganas. Así que os apetecerá pasar por El beso en la Luna, de donde he sacado estas imágenes y donde publican preciosas fotos astronómicas en 3D. ¡Muy recomendables!
