Categoría: Ciencia

Artículos de divulgación científica.

De la T4 a Madrid: zonas favorecidas y maltratadas

Iñaki Úcar1 comentario

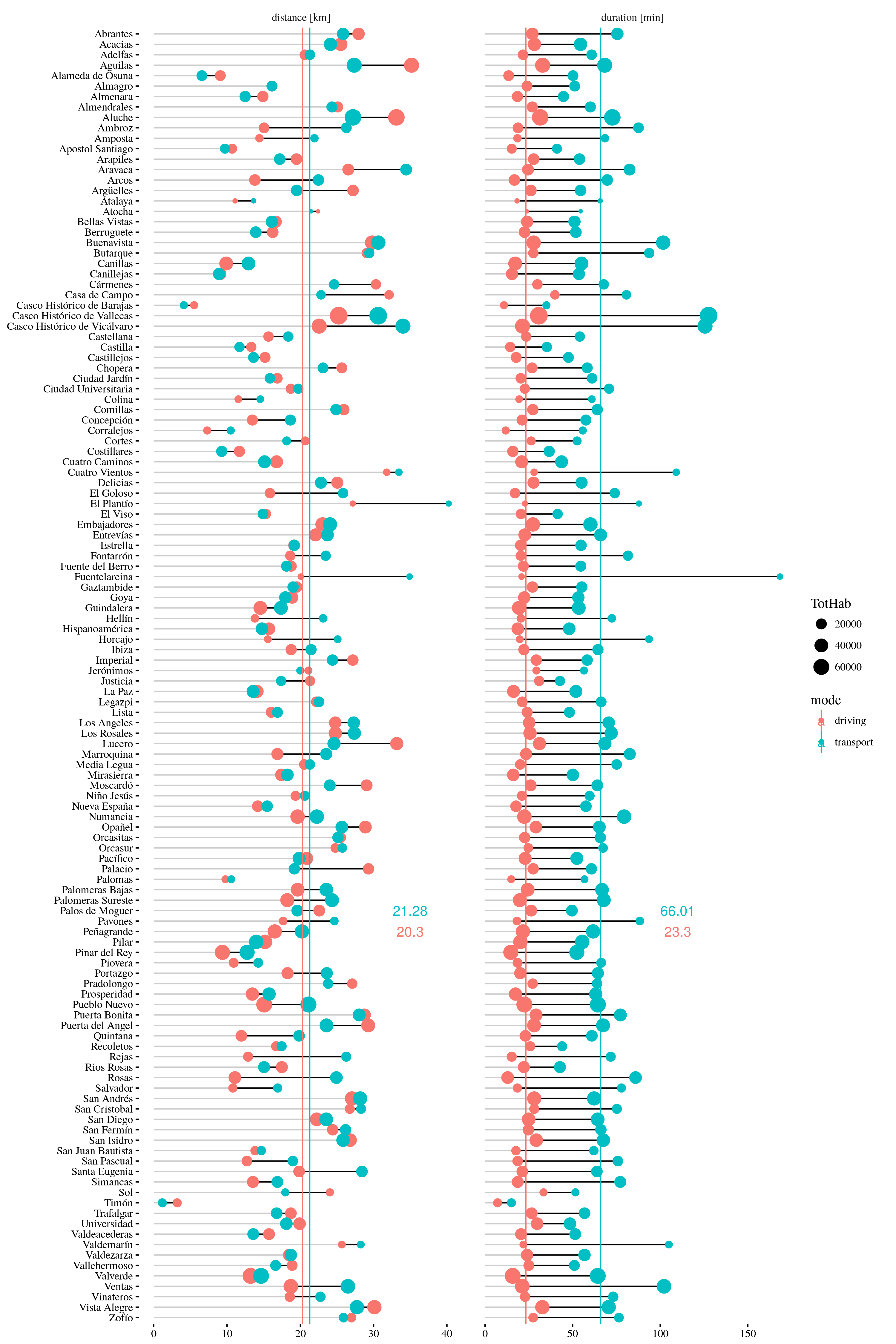
Por sugerencia de Almudena, continúo el artículo de ayer, De la T4 a Madrid: ¿coche o transporte público?, con otra gráfica interesante: el tiempo de viaje vs. la distancia al aeropuerto. Del mismo modo que en dicho artículo, cada punto representa un barrio, con el tamaño del punto proporcional a su población. Además, las regresiones están ponderadas por población.

bap2

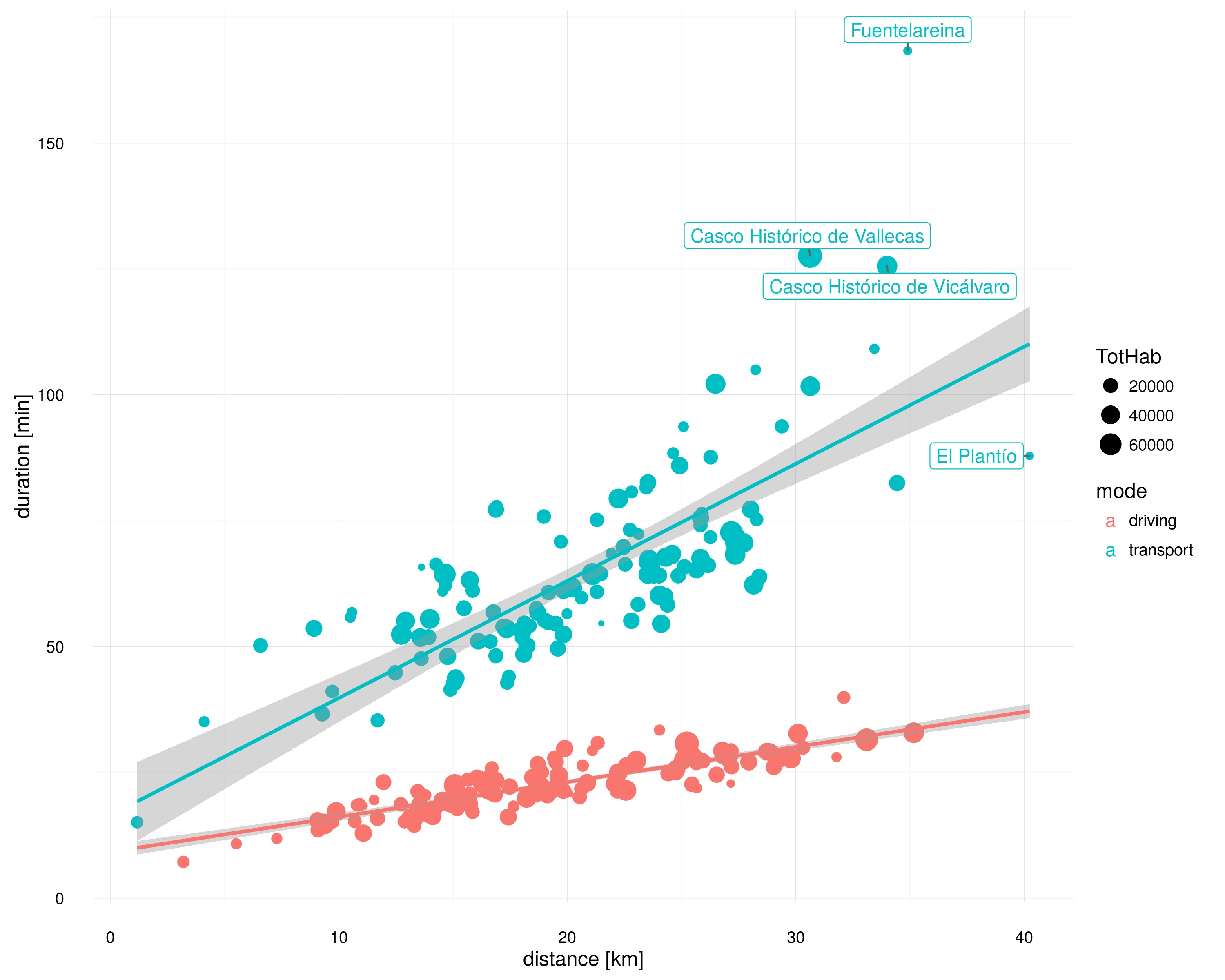
La información que nos proporciona es qué barrios están mejor o peor comunicados. En principio, esperamos que el tiempo aumente proporcionalmente con la distancia, como ocurre en el caso del viaje en coche. En el caso del transporte público, la pendiente es mayor, por lo que un aumento de distancia penaliza más en tiempo, cosa que también es razonable.

Pero además hay puntos concretos que se alejan sustancialmente de la línea por abajo (lo que significa que están especialmente bien comunicados) o por arriba (lo que significa que están especialmente mal comunicados). En la primera categoría, destaca El Plantío, un pequeño barrio del distrito de Moncloa-Aravaca que es el más lejano de Madrid, pero se encuentra especialmente bien comunicado. En la segunda categoría, destacan Fuentelareina, Vicálvaro y Vallecas. El primero tiene poca población, pero Vicálvaro y Vallecas son dos de los barrios más grandes de Madrid, y sin embargo cuentan, comparativamente, con las peores conexiones en transporte público con la terminal T4.

Actualización

Me comentan por Twitter que la conexión desde Vallecas no es tan mala. Efectivamente, una consulta a mano desde zonas razonables del barrio arroja tiempos más bajos. Compruebo en los mapas de Madrid que el territorio del barrio Casco Histórico de Vallecas es bastante amplio, pero la zona urbanizada está apelotonada en el norte y este de la zona.

Dado que los cálculos se han hecho automáticamente a partir del centroide del barrio, esto con toda probabilidad ha hecho que se sobrestimen los tiempos en barrios con una geografía poco homogénea como Vallecas. Las conclusiones, en tales casos, son erróneas.

Una mejora sencilla al método del centroide consistiría en dividir cada barrio en una rejilla de puntos, hacer los cálculos para cada punto y después descartar a partir de cierto umbral. Esto tampoco está exento de problemas, ya que podría haber un barrio con más zona sin urbanizar que urbanizada, por lo que los outliers serían los tiempos reales.

Otra mejora aún más sencilla (y rápida) consiste en dejar a Google Maps decidir dónde está «Casco Histórico de Vallecas» (que parece que no lo hace mal), y así con todos los barrios. Esto es lo que ha hecho Marco rápidamente, me ha pasado los datos y los resultados cambian sustancialmente para la gráfica anterior:

bap3

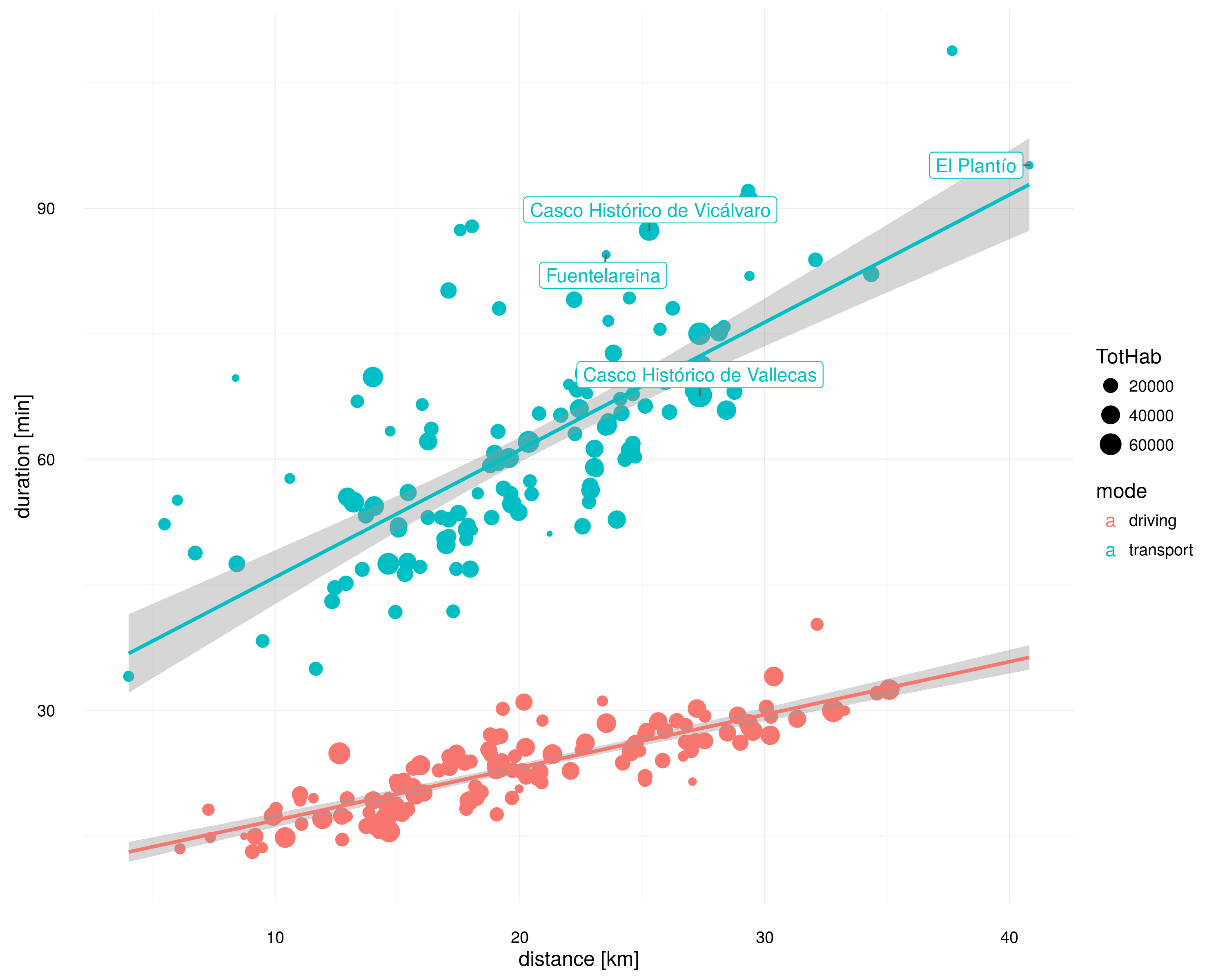
Buenas noticias: El Plantío ya no aparece como favorecido ni Vallecas como desfavorecido. Fuentelareina y Vicálvaro por su parte sí siguen situándose por encima de la tendencia generalizada. Quedaría actualizar la gráfica del artículo anterior, pero adelanto que las medias para todo Madrid se ven poco afectadas.

De la T4 a Madrid: ¿coche o transporte público?

Iñaki Úcar1 comentario

Kiko Llaneras analizaba ayer en El País el trayecto en coche y transporte público desde el aeropuerto al centro de diversas ciudades españolas en Del aeropuerto al centro: ¿en coche o transporte público? El resultado es el esperado, es decir, que en coche se tarda menos en general, pero con la salvedad de dos casos: Valencia y la terminal T4 de Madrid, donde el tiempo promedio es similar en transporte público.

En concreto, para la T4, se obtienen unos 21 y 26 minutos de trayecto para coche y transporte público respectivamente. Este resultado choca frontalmente con la experiencia cotidiana, pero hay que tener en cuenta que el dato está calculado para el trayecto hasta la parada de transporte público más cercana al ayuntamiento. En definitiva, no parece un dato muy representativo del madrileño medio y ni siquiera del turista medio que vaya hacia su hotel. De hecho, en el artículo añaden que

Mi compañero Marco Gramaglia ha hecho un análisis más extenso del asunto para la T4 de Madrid con el objetivo de obtener una media más representativa. Para ello, ha calculado la distancia y el tiempo, en coche y transporte público, desde la terminal T4 hasta cada uno de los barrios de Madrid. Después, cada barrio contribuye a la media global de manera ponderada por población:

Yo he tomado sus datos y he obtenido la siguiente figura que desglosa distancia y duración del viaje, en coche y transporte público, para cada barrio. El tamaño de los puntos es proporcional a la población del barrio y las líneas verticales marcan las medias ponderadas, cuyos valores exactos también aparecen sobreimpresos.

BAP

Como puede apreciarse en la gráfica de la derecha, la duración del viaje en coche tiene una varianza pequeña. Es decir, vayas a donde vayas dentro de Madrid, en coche tardarás un tiempo cercano a la media ponderada, que es de unos 23 minutos. Por otro lado, la duración del viaje en transporte público varía mucho en función del barrio de destino, cuya media ponderada es de más de 1 hora.

Hay pocos barrios con una media en transporte público cercana a la media ponderada global en coche. Uno de ellos, precisamente, es el barrio de Justicia, colindante con el Ayuntamiento de Madrid, de ahí que el dato obtenido por Kiko Llaneras para el caso de la T4 resulte poco representativo. Probablemente el análisis de las otras ciudades adolecerá de un problema similar, aunque lógicamente la desviación será menor en ciudades más pequeñas.

Metodología

Los diferentes barrios y sus coordenadas se han descargado de aquí; las cifras de población, de aquí. A partir de estos datos, se ha calculado el centroide de cada barrio y, con ayuda de Google Maps, se han obtenido las distancias y duraciones de trayecto desde la terminal T4 hasta dichos centroides, tanto en coche como en transporte público, para hoy 2 de agosto a las 17 horas.

Se podría refinar el análisis obteniendo los datos para diferentes días y diferentes horas, pero la diferencia promedio de duración obtenida entre ambos medios de transporte es lo suficientemente grande como para aceptar que las conclusiones no variarían.

Sobre significancia y p-valores

Iñaki Úcar1 comentario

Nada nuevo bajo el Sol, pero nunca de más que, tal y como está el panorama, la American Statistical Association puntualice estas cosas de forma oficial:

  1. Los p-valores pueden indicar cómo de incompatibles son los datos con un modelo estadístico específico.
  2. Los p-valores no miden la probabilidad de que la hipótesis bajo estudio sea cierta, o la probabilidad de que los datos se hayan dado simplemente por casualidad.
  3. Las conclusiones científicas y las decisiones políticas o empresariales no deberían basarse solo en que un p-valor supere cierto límite.
  4. Una correcta inferencia requiere información completa y transparencia.
  5. Un p-valor, o la significación estadística, no mide el tamaño de un efecto o la importancia de un resultado.
  6. Por sí solo, un p-valor no proporciona una buena medida de evidencia sobre un modelo o hipótesis.

Y ahora cogéis todos los libros que lo enseñan como la verdad revelada, todos los papers que dicen que tal o cual cosa es así o asá porque un p-valor nos salió menor que 0.05, y hacéis una pira con ellos. No sé lo que quedará, pero frío no vamos a pasar.

El canto de las pirámides, ¿genio o casualidad?

Iñaki Úcar

Dicen que la arquitectura y las matemáticas hicieron de los Mayas una gran civilización, y que prueba de ello es cómo conseguían imitar el canto del Quetzal con sus imponentes pirámides. Obviaremos por el momento el hecho de que una pirámide maciza como las mesoamericanas, sin cámaras interiores, no deja de ser una acumulación de piedras —un montón grande y ordenado, sí, pero un montón al fin y al cabo— y nos centraremos en el fenómeno en sí. Porque es cierto que, cuando se dan palmadas frente a una pirámide, como puede escucharse en el vídeo que encabeza la entrada, esta devuelve una especie de graznido similar al de algunos pájaros. Tampoco es menos cierto que esta característica no es exclusiva de las pirámides Mayas, sino que sucede en todas las pirámides mesoamericanas. El elemento común que comparten, el culpable último del fenómeno, no es otro que la escalera.

Recientemente, pudimos comprobarlo por nosotros mismos en una visita a la zona arqueológica de Cholula, en el estado de Puebla, México. Allí se encuentra la Gran Pirámide de Cholula, que se caracteriza por tener el basamento piramidal más grande del mundo. La pirámide, que ya estaba muy deteriorada por desuso cuando llegaron los conquistadores, parece hoy en día un montículo natural coronado por una iglesia, el Santuario de la Virgen de los Remedios. Varias excavaciones han puesto al descubierto diferentes estructuras de la pirámide como el Patio de los Altares, ubicado en el costado sur, en el que destaca un pequeño tramo de escaleras. Atentos al audio que grabamos, especialmente a partir del segundo 20:

La verdad es que el sonido como de una gaviota, como dice Almudena, que nos devuelve la escalera es bastante sorprendente y curioso, por lo que quizás no es raro que se haya especulado con un diseño, una intencionalidad. Pero lo cierto es que no hay nada especial en esas pirámides: cualquier escalera de piedra con peldaños de un tamaño adecuado para un humano produce ese mismo efecto. Fundamentalmente, el sonido que escuchamos de vuelta viene determinado por 1) las características tímbricas de la palmada, 2) la velocidad del sonido y 3) las dimensiones de un peldaño para humanos. La explicación es muy sencilla y tiene que ver con el amigo Fourier.

En primer lugar, una palmada prácticamente es un impulso sonoro, una señal que apenas dura unos milisegundos y que, por tanto, tiene un espectro en frecuencia muy amplio. Ese impulso viaja hacia las escaleras y va chocando con los sucesivos peldaños, que hacen que parte de la energía rebote hacia nosotros en forma de eco. Pero cada peldaño está un poquito más alejado, por lo que cada uno de ellos produce un eco un poquito más tarde que el inmediatamente anterior. El resultado es que, en lugar de recibir el eco de una palmada, como sucedería con una pared, recibimos de vuelta un tren de ecos. Y el tiempo entre ecos es similar, aparece una periodicidad, por lo que la frecuencia asociada a dicho periodo se ve reforzada: aparece un tono reconocible, una nota.

Además, sucede que el rango de tamaños en el que se puede mover una escalera da como resultado un rango de periodos audibles para nosotros. Si el tiempo entre ecos fuese exactamente el mismo, oiríamos una nota perfectamente definida y estable. El tema es que la escalera sube y nosotros estamos abajo: los rebotes se producen de forma oblicua con un ángulo cada vez mayor, por lo que, para cada escalón, la palmada viaja una distancia un poquito mayor, y la separación en tiempo del eco resultante con el anterior es cada vez un poquito mayor. Mayor separación, mayor periodo, menor frecuencia: implica un sonido descendente, que es exactamente lo que sucede.

aplauso

A la vuelta de la excursión, hice un pequeño experimento para corroborar esta explicación. Grabé una palmada e hice un pequeño script que simplemente la replica 40 veces (equivalente a 40 escalones) con un cierto retardo (equivalente a escalones de 15 cm) que va creciendo paulatinamente (tan solo unos 10.5 µs por escalón). El resultado es el siguiente:

Prácticamente el mismo efecto. ¿No es más alucinante la explicación científica que hacer cábalas sobre los misteriosos conocimientos de culturas perdidas? Para los interesados en un análisis matemático más riguroso, os recomendamos leer a N. F. Declercq et alii, «A theoretical study of special acoustic effects caused by the staircase of the El Castillo pyramid at the Maya ruins of Chichen-Itza in Mexico», J. Acoust. Soc. Am. 116, 3328 (2004).