A pesar de que el sistema de afinación pitagórico es el único que respecta las dos consonancias principales (8as y 5as), la incompatibilidad entre ambas daba lugar a bastantes inconvenientes, tal como vimos la semana pasada. Como alternativa se propusieron otros sistemas a lo largo de la historia, algunos basados en la consonancia de 3ª (como el sistema justo o el mesotónico), otros, en unidades interválicas más pequeñas que el semitono (sistema de Holder, por ejemplo). No tengo especial interés en estos sistemas, pues creo que no aportaron mucho al sistema actual, pero se puede hablar de ellos en otra entrada si alguien tiene interés. Finalmente, el sistema que se impuso fue el sistema temperado, o temperamento igual (en inglés Equal Temperament, ET), basado en 12 semitonos iguales y que sólo respeta la consonancia de 8ª. Todas los demás intervalos, como veremos en esta entrada, resultan ligeramente disonantes. A pesar de ello, es un sistema óptimo para la música tonal, especialmente a partir del Barroco y el Clasicismo: cada vez más llena de modulaciones (cambios de tonalidad o de «escala»), alteraciones accidentales, cromatismos (empleo consecutivo de intervalos de semitono), etcétera.
El semitono temperado:
Es fácil deducir la razón de ser matemática del sistema temperado. Para ello intentaremos averiguar cuánto mide el intervalo de semitono en este sistema. Un intervalo es una proporción de frecuencias, por lo que la frecuencia de cada nota de la escala cromática, se obtendrá de multiplicar la nota anterior por la proporción (razón) correspondiente a un semitono, que por el momento llamaremos «x». Si queremos saber, por ejemplo, cuál es la frecuencia de do#, multiplicaremos la frecuencia de do por «x». Para obtener re, volveremos a multiplicar el resultado obtenido por x, (o la frecuencia de do por x2), etcétera. Por tanto, si queremos completar una 8ª con 12 intervalos iguales, necesitamos un semitono tal que al multiplicarlo 12 veces consecutivas por la frecuencia base, (pongamos 1), dé como resultado una frecuencia doble, (2, el mismo sonido una 8ª más agudo). Esto es: . Por tanto,
. Esta es la relación de frecuencias correspondiente a un semitono temperado. Este semitono es intermedio de los pitagóricos: diatónico,
, y cromático,
.
La escala temperada:
Para hallar la proporción correspondiente a cualquier otro intervalo de la escala temperada, tan sólo tendremos que elevar al número de semitonos (ST) que contiene dicho intervalo. En la tabla podéis ver una comparativa entre los intervalos pitagóricos, los temperados y los consonantes. Algunas consonancias están entre paréntesis porque son resultado de la inversión de otro intervalo consonante: la 4ªJ es una inversión de la 5ªJ (de do a sol hay una 5ªJ, de sol al do más agudo hay una 4ª), la 3ªm es el intervalo que hay entre mi y sol, ambos consonancias de do, por lo que también suele considerarse consonante, por último, la 6ªM es la inversión de la 3ªm.
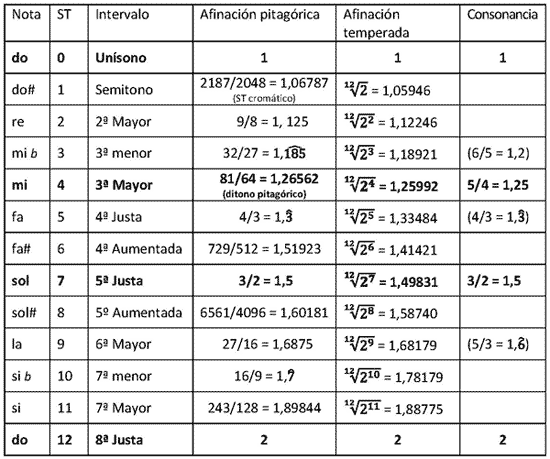
También podéis apreciar las diferencias de afinación en este gráfico extraído de la wikipedia, aunque con algunos errores corregidos del original. Los puntos negros son temperados y los azules pitagóricos. El cent es una medida de afinación equivalente a la centésima parte (logarítmica, claro está) de un semitono temperado:
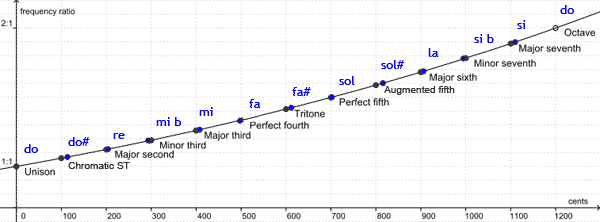
Como podéis ver, ambos sistemas son muy parecidos. Las mayores diferencias se encuentran entre las notas alteradas, especialmente al llegar al sol# (extremo del círculo de 5as). Sin embargo, si escuchamos la escala diatónica de los sonidos naturales, afinada según el sistema pitagórico o el temperado, resultan casi indistinguibles.
La 5ª Justa:
la 5ªJ temperada es casi idéntica a la pitagórica: difieren aproximadamente 2 cents. Para que os hagáis una idea, podéis escuchar cómo suenan dos sonidos que difieren en 1 cent, 6 ó 10 en esta página de la wikipedia. Son indistinguibles.
La diferencia entre ambas 5as recibe el nombre de schisma. Para calcular cuánto mide basta dividir la 5ª pitagórica entre la temperada, o bien, repartir la coma pitagórica entre las 12 quintas que cierran el círculo en el sistema temperado. El resultado es el mismo:
La 3ª Mayor.
La 3ªM difiere algo más entre un sistema y otro, pero sigue siendo claramente disonante en ambos. Hasta no oírlo, yo no imaginaba cuanto, así que aquí tenéis el intervalo afinado en ambos sistemas y una 3ªM consonante para compararlos.
Para escuchar más posibles comparaciones, resulta muy útil el programa Scala del que nos habló Zarlino y cuya recomendación yo reitero.
Actualmente se ha impuesto el sistema temperado en la industria y en los instrumentos de teclado y electrónicos, en efecto.
Sin embargo, en la interpretación de música vocal se ha impuesto definitivamente el sistema justo, y no solamente por parte de grupos muy especializados como Oxford Camerata, http://es.wikipedia.org/wiki/Oxford_Camerata para música antigua, sino de toda la música de tradición oral, el canto «de barbería», la música celta, etcétera. El motivo es la fuerza increíble de la consonancia de las terceras y quintas, en que al encajar perfectamente las frecuencias, tienden a reforzar el sonido de los acordes, sin el compromiso de tener que modular a tonalidades lejanas o limitarse a doce notas como en los otros casos.
Las restricciones mencionadas que han hecho imponerse al sistema temperado son artificiales, provienen del romanticismo occidental, y al ignorarlas cuando ello es posible se suele ganar en variedad sonora.
Iñaki me ha contado que el director de su banda también suele intentar que afinen las 3as «más pequeñas» y las 5as algo más amplias en pos de la consonancia. Pero, como bien dices, no es posible hacer esto en los instrumentos de afinación fija o en obras con demasiadas modulaciones o modulaciones a tonos lejanos.
Precisamente, en el sistema justo, al intentar normalizarlo (al intentar fijar la afinación de las notas independientemente de la tonalidad en la que nos movamos, para poder aplicárselo, por ejemplo, a un teclado) surgen bastantes irregularidades. Hay que reducir una de cada cuatro quintas, los tonos de la escala tiene dos tamaños distintos etc. Por no mencionar que el sistema varía dependiendo de si se basa en la 3ªM o en la 3ª menor. En otra entrada puedo hablar de ello.
Por otra parte, no conocía la Oxford Camerata. Le estoy echando una oreja en spotify y tiene muy buena pinta. ¡Gracias por la recomendación!
Los cuartetos de cuerda también lo hacen habitualmente, si quieren sonar bien. Los instrumentos de viento que producen la tercera como armónico 10, dan una tercera baja, justa, a no ser que apliquen la corrección pertinente de forma consciente. En cambio los pasajes melódicos como las escalas se hacen más bien pitagóricos, o sea, con terceras grandes y segundas menores pequeñas. Por tanto usan dos sistemas al mismo tiempo, dependiendo de si la tercera es melódica o armónica, será más alta o más baja, y se suele tomar el bajo (el violoncello) como referencia para el oído.
La coexistencia de los dos sistemas entre instrumentos diferentes hace que el problema de la afinación perfecta no tenga solución, por más que los teclados y pianos lo tengan resuelto. Y el coste de que no esté resuelto es que los dos tipos de tercera sonando a la vez producen unos batidos muy desagradables.
Afortunadamente nuestro oído tiene una tolerancia alta a estos problemas, en caso contrario no soportaríamos la música de banda, de hecho hay quien no la soporta :-)
@Paco: No entiendo lo del armónico 10. El armónico 10 es la misma tercera que el armónico 5, pero una octava por encima. Por otra parte, todos los instrumentos producen armónicos justos, es inevitable. Por eso las distintas afinaciones a la afinación justa o natural producen batidos.
Tampoco sé por qué dices lo de la banda. Las bandas afinan con afinación natural. Se tiende a cerrar las terceras mayores, abrir las terceras menores y abrir las quintas. Y las orquestas hacen lo mismo, a no ser que toquen con piano.
Sí, el 5 y el 10, por supuesto. Como sabes, en la zona 8 – 9 -10 hay notas de la escala seguidas, en cambio 4 – 5 – 6 son saltos de tercera. Si un instrumento como el trombón puede hacer una escala con 8 – 9 – 10 sin mover la vara, no lo hará usando el 5 y moviendo la vara continuamente.
Las bandas afinan con afinación natural… sí. Cuando afinan. La relación entre música de bandas (la típica música de banda vocacional, no profesional) y tolerancia del oído, es una relación estrecha. Sin ánimo de ofender.
¿No te das cuenta de que quería hacer un chistecillo ordinario? Para eso están los smileys, Iñaki, por Dios.
Iñaki > Por otra parte, todos los instrumentos producen armónicos justos, es inevitable.
Sí, pero no me has leído bien, yo dije
Paco > Los instrumentos de viento que producen la tercera como armónico 10, dan una tercera baja
Porque los instrumentos que producen la tercera con una llave afinada por el sistema temperado, no dan una tercera baja, sino temperada.
@Paco: Ok, pero sigo sin entender qué quieres decir con esto último… :-?
Ay, Señor, Señor… ¡Qué pruebas me envías…!
Pues quiero decir, remitiéndome al primer comentario, que lo de «el sistema temperado se ha impuesto» es sólo parcialmente cierto, como hemos visto varios sistemas coexisten aunque el ‘oficial’ sea el temperado.
Dije que los instrumentos QUE AFINAN la tercera como armónico, no la dan temperada. Contraejemplo primero.
Pero me entendiste mal, así que tuve que repetir la frase y decir que si usan llaves, AFINAN esa tercera temperada. Contraejemplo del contraejemplo primero, para aclarar que aunque es cierto que los armónicos son justos, las llaves existen y eso no invalida que los sistemas se mezclan como yo decía.
@:Paco Supongo que con «bandas» te referías a algo así… aunque también hay orquestas bochornosas, créeme
Corregidme si me equivoco, pero hasta donde yo sé:
(a) Los sintetizadores permiten utilizar escalas justas todo el tiempo porque van ajustando las frecuencias para que queden lo más ‘armónicas’ posibles… Armónicas en el sentido pitagórico, o sea, relaciones de frecuencias como cocientes de números enteros bajos.
(b) El que nuestros instrumentos den espectros con componentes en forma de múltiplos enteros de la fundamental es una cuestión constructiva. Toda la música indonesia se basa en instrumentos con espectros ‘irracionales’ y por tanto tienen armonías totalmente distintas… que a ellos les suenan ‘bien’.
@Zarlino: (a ver si te he entendido)
a- La verdad es que no sé cómo funciona un sintetizador. Pero, para que todo el tiempo diese intervalos consonantes, la afinación de cada nota estaría variando constantemente, con cada acorde nuevo. Supongo que sí es posible.
Por otra parte, yo conozco como sistema de afinación «justo» un sistema que respeta la 3ªM consonante, pero se carga las 5as…
b- Todos los objetos que suenan y son «unidimensionales» (una cuerda, un tubo cilíndrico, como el clarinete, o cónico, como el saxo) lo hacen de modo que los armónicos de su sonido, son múltiplos y submúltiplos de la frecuencia natural del objeto. Es lógico e inevitable: una cuerda sujeta por los extremos vibra de muchos modos a la vez, pero siempre tiene dos nodos en esos extremos: por eso vibra por mitades, tercios etc. y produce los armónicos correspondientes. Los objetos bidimensionales o tridimensionales (véase instrumentos de percusión) tienen más ejes de simetría posibles así que producen sonidos no perfectamente armónicos, o con varias series de armónicos no consonantes entre sí (échale un vistazo a esto). A algunos de estos sonidos se los llama semirruidosos y el oído extrae su frecuencia de mala manera (por ej: un timbal se puede afinar, pero su frecuencia no es tan «clara», tan discernible, como la de una cuerda de un violín, por ejemplo). Los sonidos con una frecuencia «clara» es lo que Helmholtz llamó sonidos musicales: sus armónicos corresponden a distintos modos de vibración del objeto y sus frecuencias son múltiplos de la principal (viento, cuerda). Los sonidos con un espectro caótico son ruidosos (platillos, gong etc).
Me extraña que puedas basar todo un sistema musical en sonidos ruidosos o semiruidosos. Entre otras cosas, es difícil percibir claramente la frecuencia de estos sonidos, por lo que no serían muy útiles a la hora de entonar melodías (salvo excepciones: marimbas, xilófonos etc). Podrían tener una función como acompañamiento percusivo en la música, por ejemplo. En cualquier caso, me consta que la música oriental también utiliza instrumentos de cuerda.
Desde mi punto de vista (aunque esto es sólo una opinión), la percepción de la consonancia (una frecuencia y sus múltiplos) es una cuestión adaptativa. Si las cosas suenan así (nuestra voz misma suena así) y esto nos resultase desagradable, nos volveríamos locos. Creo que si la polifonía volviese a desarrollarse (o unos marcianos con nuestro mismo sistema perceptivo la desarrollasen por su cuenta) volvería a aparecer el mismo sistema musical. Además, existe un motivo puramente fisiológico para la disonancia, bastante comprensible: el oído invierte más energía en distinguir dos sonidos de frecuencias muy próximas, que en dos sonidos claramente diferentes. Otros sonidos son disonantes porque chocan sus armónicos. Véase do-sol# (choca el segundo armónico de do: sol con el primero de sol#: sol#), o do-si (choca el 3er armónico de do:do, con el 1º de si:si) etc.
Por otra parte, por lo poco que sé de la música oriental, es tradicionalmente monódica (como la música folklórica de todas partes, por otro lado), así que es posible que su sistema musical sea muy diferente al occidental. Lo que no creo es que su percepción de la disonancia y la consonancia sea muy distinta a la nuestra: quizás haya cosas que nos suenen «raras» o exóticas y viceversa, pero no nos dañarán el oído, ni nos estresarán. Por lo general, incluso me atrevería a opinar que interpretaríamos de forma parecida la «intención» de esa música (sensualidad, alegría, exaltación, miedo etc). Si no, las bandas sonoras de las películas tendrían que traducirse en cada país… Pero esto también es una opinión, no lo he comprobado, claro.
Ah, se me olvidaba. A ver si nos puedes recomendar algo sobre música indonesia. Yo conozco muy poco. En la Complutense tenemos una biblioteca de música (¿musicoteca?), en la que cogí algún disco… pero me gustaría saber más sobre estas tradiciones.
@Zarlino: En la música de los Gamelan de Java se escuchan timbres inarmónicos, lo que no quiere decir que sean ruidosos según la definición acústica de ruido. Su espectro no es continuo sino que presenta picos, tienen parciales como los sonidos de nuestras cuerdas y tubos, pero no siguen la serie armónica y, en efecto, esto no ayuda a nuestra percepción de altura tonal. Más que sonarles «bien» sospecho que la nuestra a su lado debe parecerles «sosa» y no me extraña, pues nos hemos ido polarizando hacia melodías y acordes, mientras que ellos emplean texturas y «nubes sonoras» que evolucionan de otra manera. Cada sonido no tiene en absoluto el significado que en nuestra música tiene una nota de un acorde.
Esta tímbrica tiene su sustento en el empleo de instrumentos percusivos de formas no simples. Si usaran mayoritariamente instrumentos de cuerda y/o viento, todo sería distinto, sonaría más occidental, por lo que ha dicho Almudena de su carácter geométricamente unidimensional a grandes rasgos.
Podríamos pensar ingenuamente que es una música «desafinada», pero nuestro concepto de afinación es sumamente ajeno a esa música, por lo que se trata de una desviación sólo para nuestros oídos. En ese sentido sí, a ellos les suena bien.
Piensa también en el concepto de belleza que tiene el arte de cualquier otra cultura, no se aplican nuestros parámetros y no se puede comparar directamente.
Y respecto al punto a), los sintetizadores efectivamente ofrecen control total sobre la frecuencia, por definición, así que puedes usar (si eres capaz de controlarlo adecuadamente) sonidos pertenecientes a cualquier sistema de afinación.
Entonces sí se pueden tener terceras justas y quintas siempre perfectas, el problema del sistema justo de «estropear» algunas quintas desaparece, y como resultado tenemos un montón de sonidos, y no solamente doce, que es de donde viene el problema del sistema justo de afinar los teclados.
Las fracciones pitagóricas no son especialmente buenas como intervalos armónicos, supongo que te refieres a otros teóricos precursores de la justa entonación, como Aristógenes o Zarlino. ¡Hombre, qué casualidad!
Paco, lo has expresado divinamente. Gracias por aclarar lo que yo intentaba decir. Por lo que he oído hay sintentizadores que van ajustando los sonidos en tiempo rela para que las tríadas queden justas-justas, lo cual implica que hay más de doce sonidos… pero eso es lo que hacen los cantantes de música antigua. En cuanto a lo de los indonesios, pues eso, lo que tú dices. Simplemente quisiera corregir a Almudena y decirle que una barra rígida unidimensional que vibra librmente emite frecuencias anarmónicas (al resolver la ec de Euler-Bernoulli salen autovalores no enteros). De hecho salvo para cuerdas y tubos »’ideales»’ lo de las series armónicas es un camelo… como, creo yo, lo de que la percepción de la consonancia y disonancia es universal para todos los seres humanos en todo tiempo y lugar.
Disiento. La consonancia y la disonancia son universales. Nuestros grados de tolerancia o su uso en el arte sí pueden variar hasta cierto punto con la cultura. Lo cual no significa que no las percibamos. A mí me puede gustar más o menos la sal, por poner un ejemplo paralelo, en función de la gastronomía que se estile en mi pueblo, pero mi lengua y la de un chino reaccionan igual a ella.
De hecho, la disonancia tiene una función fundamental en la música: sirve para crear tensión, movimiento, interés. Precisamente la palabra elegida por Paco me gusta: una música sin disonancia alguna puede sonar «sosa» porque la consonancia constante es demasiado estable. Que toleremos esa disonancia en ciertos grados (puesto que hay grados y grados de disonancia: una 2ªm es mucho más disonante que una 7ªM), no significa que la disonancia sea subjetiva o dependa enteramente de la cultura. Existe un motivo fisiológico para su existencia. Y existe un motivo también para que ciertas irregularidades en las series armónicas o cierto grado de desafinación no nos produzcan tampoco demasiada tensión. Iñaki lo explicaba en su segundo artículo de física de la consonancia.
Piensa en la banda sonora de una peli de terror: ¿crees que la tensión que nos producen esos sonidos, (generalmente llenos de disonancias muy fuertes), dispuestos de esa manera, es una cuestión puramente cultural? ¿Se deben sólo a la utilización de un idioma armónico en el que hemos sido educados? ¿En otra cultura la utilizarían en una sesión de relajación o de musicoterapia?
@Zarlino: Supongo que con «anarmónicas» quieres decir «inarmónicas» o «parciales discordantes», como suele decirse. Bien. Puntualizo:
Las vibraciones en varillas sólidas pueden ser de tres tipos: transversales, longitudinales o de torsión. En las vibraciones transversales (como en una cuerda), y como bien dices, aparecen parciales discordantes, es decir, frecuencias múltiplos no enteros de la fundamental, pero es que una varilla rígida no puede considerarse un objeto unidimensional, puesto que hay que considerar que las partes externas e internas sufren tensiones contrarias. En cambio, si una varilla se frota en sentido longitudinal, aparecen vibraciones longitudinales y aquí sí podemos simplificar y considerarla un objeto unidimensional. En este caso, los armónicos son múltiplos enteros de la frecuencia fundamental.
Lo de las series armónicas no es ningún camelo.
@Almudena: Creo que hasta el siglo XIII las terceras eran consideradas disonantes y ahora no lo son; lo mismo ocurre con muchos acordes del jazz que hace cien años sonaban a rayos y ahora aparecen en casi cualquier ‘canción del verano’. Es a eso a lo que me refería, pero acepto tu puntualización porque al fin y al cabo sabes más que yo de estas cosas.
@Iñaki: Cualquier cosa que vibre lo hace de las tres maneras, y aunque lo hiciera sólo de una, el aire que lo transmite vibra longitudinalmente… pero de forma no totalmente adiabática, por lo que aparecen retrasos histeréticos. La ‘ganancia’ de nuestro oído no es tal porque contiene términos claramente no lineales (dependen maonmeno del cubo de la amplitud). En consecuencia, corrijo lo del ‘camelo’: las series de Fourier son una estupenda herramienta matemática, pero no son la realidad.
Precisamente: existe una evolución lógica en la historia de la música. No encontrarás un sistema de hace mil años basado en las 2as menores, que consideren las 5as disonantes. La 3ª tardó más en ser aceptada, porque, de hecho, es más disonante que la 5ª. Antiguamente no tenían forma de saber cómo impresionaba el sonido nuestro oído y, sin embargo, los sistemas musicales ya seguían un patrón basado en la mayor consonancia posible. Esto no quiere decir que no haya cierto margen para el gusto: sabemos que una 7ª es más disonante que una 5ª, pero siempre podemos decidir cómo y cuánto utilizarla.
En cualquier caso pienso que hay dos niveles para el gusto: una cosa es que no disfrutes escuchando algo porque no te identificas con ello (no es parte de tu cultura). A mí no me gusta… la música de salsa, por ejemplo, o el reggaeton. Y otra cosa es que realmente te resulte insoportable, te estrese. Dudo mucho que a la gente del siglo IX le estresasen demasiado las 3as (aunque no he hablado con esa gente, claro): existía un canon estético que decía que eran de mal gusto, unas reglas de composición determinadas, esa música no estaba de moda, por decirlo así… pero de ahí a que les sonase MAL, a que no pudiesen soportarlo, hay un trecho.
Eso no quita que, por supuesto, también haya cierto margen de adaptación. El jazz, como dices, es mucho más disonante que otros estilos de música (aunque siempre utiliza la disonancia de manera controlada), por lo que probablemente alguien no acostumbrado a escucharlo, se pueda perder, o le suene «raro».
En cuanto a lo de los tubos, personalmente no conozco el fenómeno e Iñaki está aislado de la civilización. En cualquier caso, me atrevo a intuir (quizás me equivoque): que existan ciertas irregularidades no significa que no se pueda extraer o percibir un patrón más significativo ¿no? A fin de cuentas, nuestro sistema auditivo tampoco es «ideal»: tiene ciertas irregularidades y no puede ser perfectamente preciso.
En mi modesta opinión, la disonancia ha desaparecido como elemento de contraste en el lenguaje musical. Postulo que una vez iniciado el siglo XX, el 99% del tiempo de la música clásica y luego del jazz, así como gran parte del Pop, los acordes son disonantes.
La disonancia puede ser una sensación universal, pero no un elemento universal de significado musical, y no se puede subestimar el tremendo peso de la cultura y la tradición en la evaluación de la disonancia.
Hoy día, creo que en una obra contemporánea un acorde justo y consonante, sería tan radical como un cuadro blanco sobre blanco, o un silencio de treinta segundos. Hay muchos más elementos de contraste y factores de tensión: tímbricos, dinámicos, agógicos, formales, texturales. La disonancia es una sensación básica pero interpretable, que tenía mucha importancia en la Edad Media, pero que ahora está bajo siglos de evolución.
Respecto a las simplificaciones que se hacen en las típicas lecciones de acústica para músicos y que nos hacen calificar las cuerdas y los tubos como unidimensionales, son necesarias si queremos soslayar parte de la complejidad matemática del asunto. En la práctica violinística observamos las vibraciones longitudinales y de torsión cuando el arco hace «chirriar» la cuerda. Al observar los espectros de sonidos reales vemos que hay ruidos que no se explican por las series de Fourier. Las irregularidades microscópicas de todos los objetos, por más que nos esforzemos en crearlos geométricamente perfectos, introducen un elemento de «caos» en el sonido, al que estamos acostumbrados y cuya ausencia nos desagrada en muchos sonidos sintéticos.
@Paco: Las series de Fourier no tienen que explicar nada, son una herramienta, no una ley.
Decir que la disonancia ha desparecido como elemento de contraste sí que es soslayar la mayor parte de la música que se hace hoy en día. Otra cosa es que antes se usase el contraste entre «consonancia» y «un poquito de disonancia» y ahora ese contraste sea entre «un poquito de disonancia» y «mucha disonancia». Precisamente ahí está la evolución, y desde luego que el grado de disonancia se usa como elemento contrastante. Me atrevo a decir que dejar de hacerlo sería un gran error, puesto que es la herramienta más poderosa en materia de contrastes, sólo igualada por los matices dinámicos.
Y aquí es donde llega la polémica, claro. Habría que ver hasta qué punto puede modificar nuestra percepción esa carga cultural. Hay un motivo por el cual, la música dodecafonista, serialista… vanguardista en fin, utilizada en un medio «popular» o universal como el cine, cobra significados asociados a la tensión, el miedo, la demencia etc. No te encontrarás una escena de un picnic con música de Schoenberg.
Existen distintos grados de disonancia y no es lo mismo la disonancia «formal» (donde las 7as son terriblemente disonantes) que la disonancia perceptiva (donde una 5ª muy grave puede ser disonante y una 2ª aguda, puede que no). En el jazz esa disonancia se controla y se resuelve, lo mismo que ocurre en la música «popular», de modo que resulta digerible. Es la música de vanguardia la que hace un uso totalmente indiferente de ella.
Llegados a este punto del debate, dos cosas: (a) Cedo mi voz y mi voto a Paco, con quien estoy 100% de acuerdo y que se explica mucho mejor que yo y (b) ¿Cuándo llegan las nuevas entregas de ‘Música y Matemáticas’? Los que sabemos cuatro cosillas de esto (o menos aún) estamos aprendiendo mucho con ellas y con los debates que suscitan… Ánimo y al toro!
Sip, habrá que ponerse con ellas. La verdad es que después de hablar de afinación y escribir sobre el sistema temperado es como si hubiese llegado a una especie de «meta» y cuesta elegir por donde retomar el tema. Pero pronto vendrán más, seguro. Lo que sí es seguro es que tendremos que escribir una en concreto sobre música «culta» contemporánea, o de vanguardia. Ahí seguro que habrá polémica de la buena ;) .
Bueno, a mí me habría gustado que hubieseis hablado un poco de cómo todo esto se desdibuja utilizando sonidos con espectros inarmónicos y aparecen paradojas «escherianas» como escaleras infinitas (tonos de Shepard) y progresiones que suben y bajan a la vez (paradoja tritonal), etc… También me gustaría saber algo más de las escalas con más o menos intervalos… Lo que enlazaría con la música de vanguardia.
Aporto mi granito de arena con un enlace a http://murashin.sakura.ne.jp/en/ donde nos muestra diversas obras interpretadas con afinaciones no equiespaciadas pero más próximas al original.
En el violín la falla de la escala de Pitagoras es gritante. El violín se afina por quintas, pero resulta que la suma de dos quintas no es igual a la suma de una cuarta y uns sexta, dee manera que si se afina un mi con respecto a la cuerda sol, resulta desafinado en relación a la cuerda la. Conclusión: no queda más que usar la escala temperada. Pero lo que no logro saber es quién la inventó, ni cuando fue inventada.
@Carlos: Lo bueno que tiene el violín (viola, cello y contrabajo) es que puedes poner el dedo (menos en las 4 notas al aire) un poquito más arriba o un poquito más abajo para buscar la afinación natural. El mismo oído te lleva.
El Sistema temperado es el más perfecto que existe. Soy violinista y no me convence la afinación justa, sobre todo cuando tocamos con la orquesta sinfónica, donde la mayor parte de los instrumentos son temperados, para mí lo más perfecto es el temperamento igual de las 12 notas, sobre todo cuando hay que hacer muchas modulaciones con el instrumento solo. En ese caso no funciona la afinación justa.-
Así sonais los violines… desafinais tocando solos en casa
no sale bien las respuestas o la informacion no es todo verdadero y le faltan cosas
@Iñaki: no sabes nada de los violines ni siquiera sabras tocarlo
@Gustavo:
Gustavo deberias darle un vistazo a la musica de la india. Ellos llevan milenios usando la teoria de la afinacion justa y no tienen ningun problema con las modulaciones, ademas, aprovechan cosas que nosotros ya de plano descartamos como la combinación de tonos que ellos llaman «sananana» y , según, los datos historicos dicen que fue descubierto hace mas de 5000 años (muchos más de los que tiene Tarttini); dicha combinacion de tonos es capas de producir sinfonias completas en escala justa con tan solo tocar dos notas -cosa que no sucede con la temperada igual puesto que al combinar los tonos de dicha entonación solo se producen glissandos y no notas justas. Por otra parte la armonía en la entonacion justa es más alta que en la temperada igual y es comprobable según la formula matemática de la armonía: Valor armónico = a la división del tono fundamental entre el promedio de las frecuencias que intervienen en el tono secundario al cual deseamos obtener su valor armónico con respecto al tono fundamental (Valor armónico=(1/[f1+f2/2]) ), y por si fuera poco amplios estudios hechos en animales por David Bruce Huges comprueban que la entonación temperada produce más alteración en sus conductas al contrario de la entonación justa; cabe recalcar que, la entonación temperada es artificial y tiene como única utilidad práctica la facilitación de transporte de una melodía (no es lo mismo afinar un clavesi para un tenor, que para una soprano); y por último los estudios revelan que la mayoria de las especies cantoras como aves, delfines, ballenas, etc. son propensas a emplear escalas de entonación justa, mas sin embargo, por otra parte, ninguna especie utiliza la entonación temperada.
En conclución: la entonación temperada es útil para transportar melodias, pero, armonicamente es un desastre; y la entonación justa es excelente armonicamente hablando, más sin embargo, es un desastre para transportar melodias.
Así que… hagan sus apuestas. JAJA
Perdón, arriba quise decir «que ninguna especie, excepto el humano, utiliza la entonación temperada igual» (ojala sirva de consuelo).
@Radhanath: Me interesa lo que cuentas del uso de escalas por parte de los animales (y la verdad es que me sorprende). ¿Tienes más información o algún libro/artículo/texto que pueda leer al respecto?
@Almudena:
Estimado Almudena, yo soy alumno de el maestro Udhava Dasa que a su vez es alumno de el Gurudeva Dasanudas Bababaji (más conocido como David Bruce Hughes), quien hizo su tesis sobre un nuevo tipo de entonación llamado «Vaisnava entonation» buscalo por la red hay bastante material publicado por este Guru y si no encuentras pues tan solo ponte a escuchar a las aves (en serio), ninguna usa la escala temperada; además como dato curioso sus cantos llevan patrones rítmicos que son muy fáciles de decifrar con las Talas indues
Amigos. Es normal que tengamos diferencias en cuanto a los sistemas de afinacion y temperamentos existentes.
Ahora Si nos enfocamos en los instrumentos de una orquesta sinfónica (excluyendo un poco el piano, xilófono y todos aquellos que funcionan enarmonicamente) y pensamos y por ejemplo una 3 sinfonía de Brahms, o 5 de beethoven… Un cuarteto de cuerdas de schubert o dvorak. Un quinteto de maderas o metales (muy buena música existe para estos ultimos). Todos estos podemos y debemos afinar y «desafinar» dependiendo de la tonalidad en que nos encontremos (sea en un movimiento o pasaje del mismo movimiento en otra tonalidad).
Lo que quiero decir con esto es que debemos «donde se pueda» buscar y encontrar una afinación no tan temperada como los afinadores que existen por ahi para toda la musica…
Ok, si interpretamos el concierto num 2 de Rachmaninoff ajuro debemos temperar con el piano, pero si hacemos la muerte y la doncella de schubert (cuarteto de cuerdas) como carajo (disculpen la expresión) vamos a afinar con el temperamento de 12 notas. Un ejemplo corto, escuchen la versión mas popular que es la del cuarteto Amadeus, vayan al 2 mov. SEÑORES LAS TENSIONES JAMAS SE CREARÍAN TAN INTENSAS CON EL «APARATICO» ESE QUE VENDEN.
Ahí no hay un piano u otro instrumento que nos obligue a una afinación «estandar», entonces (a lo que quiero llegar) porque no se practica la afinación depende de lo que toquemos y que instrumentos se involucran… Se escucha complicado, pero quien dijo que la música es fácil? A veces conseguir 3 segundos de satisfacción cuesta horas, meses y hasta años (los músicos o grandes oyentes me entenderán de lo que hablo)
Como unan sensible la vamos a tocar igual que una sub dominante en distintas tonalidades. JAMAS!!! Solo por dar un ejemplo.
Espero abrir un tema muy interesante y que dejen sus opiniones. Porque «creo» que debemos buscar el máximo de una personalidad, color, sentimiento y cuantos adjetivos se les ocurra a cada tonalidad. Sino porque beethoven fue con Do menor como lo fue, Mozart con Re menor, etc, etc, etc…
gracias de veras ma ayudaste resto la informacion es muy completa
en serio