Etiqueta: música y matemáticas

A pesar de que el sistema de afinación pitagórico es el único que respecta las dos consonancias principales (8^as y 5^as), la incompatibilidad entre ambas daba lugar a bastantes inconvenientes, tal como vimos la semana pasada. Como alternativa se propusieron otros sistemas a lo largo de la historia, algunos basados en la consonancia de 3ª (como el sistema justo o el mesotónico), otros, en unidades interválicas más pequeñas que el semitono (sistema de Holder, por ejemplo). No tengo especial interés en estos sistemas, pues creo que no aportaron mucho al sistema actual, pero se puede hablar de ellos en otra entrada si alguien tiene interés. Finalmente, el sistema que se impuso fue el sistema temperado, o temperamento igual (en inglés Equal Temperament, ET), basado en 12 semitonos iguales y que sólo respeta la consonancia de 8ª. Todas los demás intervalos, como veremos en esta entrada, resultan ligeramente disonantes. A pesar de ello, es un sistema óptimo para la música tonal, especialmente a partir del Barroco y el Clasicismo: cada vez más llena de modulaciones (cambios de tonalidad o de «escala»), alteraciones accidentales, cromatismos (empleo consecutivo de intervalos de semitono), etcétera.

El semitono temperado:

Es fácil deducir la razón de ser matemática del sistema temperado. Para ello intentaremos averiguar cuánto mide el intervalo de semitono en este sistema. Un intervalo es una proporción de frecuencias, por lo que la frecuencia de cada nota de la escala cromática, se obtendrá de multiplicar la nota anterior por la proporción (razón) correspondiente a un semitono, que por el momento llamaremos «x». Si queremos saber, por ejemplo, cuál es la frecuencia de do#, multiplicaremos la frecuencia de do por «x». Para obtener re, volveremos a multiplicar el resultado obtenido por x, (o la frecuencia de do por x²), etcétera. Por tanto, si queremos completar una 8ª con 12 intervalos iguales, necesitamos un semitono tal que al multiplicarlo 12 veces consecutivas por la frecuencia base, (pongamos 1), dé como resultado una frecuencia doble, (2, el mismo sonido una 8ª más agudo). Esto es: . Por tanto, . Esta es la relación de frecuencias correspondiente a un semitono temperado. Este semitono es intermedio de los pitagóricos: diatónico, , y cromático, .

La escala temperada:

Para hallar la proporción correspondiente a cualquier otro intervalo de la escala temperada, tan sólo tendremos que elevar  al número de semitonos (ST) que contiene dicho intervalo. En la tabla podéis ver una comparativa entre los intervalos pitagóricos, los temperados y los consonantes. Algunas consonancias están entre paréntesis porque son resultado de la inversión de otro intervalo consonante: la 4ªJ es una inversión de la 5ªJ (de do a sol hay una 5ªJ, de sol al do más agudo hay una 4ª), la 3ªm es el intervalo que hay entre mi y sol, ambos consonancias de do, por lo que también suele considerarse consonante, por último, la 6ªM es la inversión de la 3ªm.

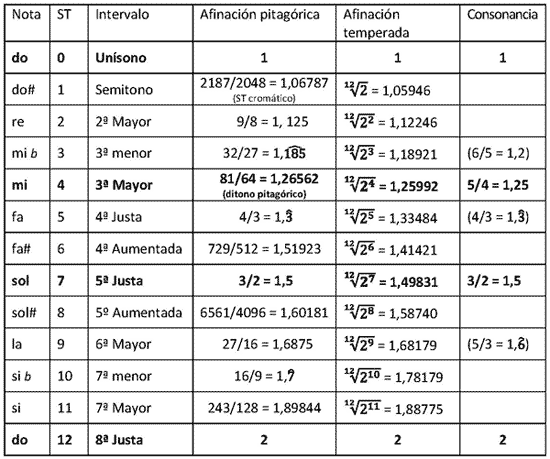
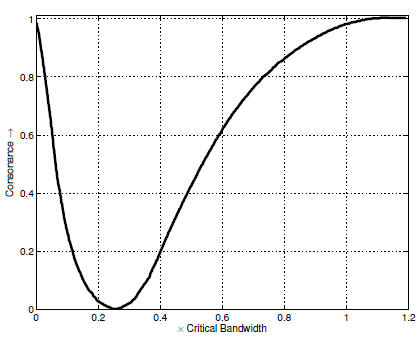
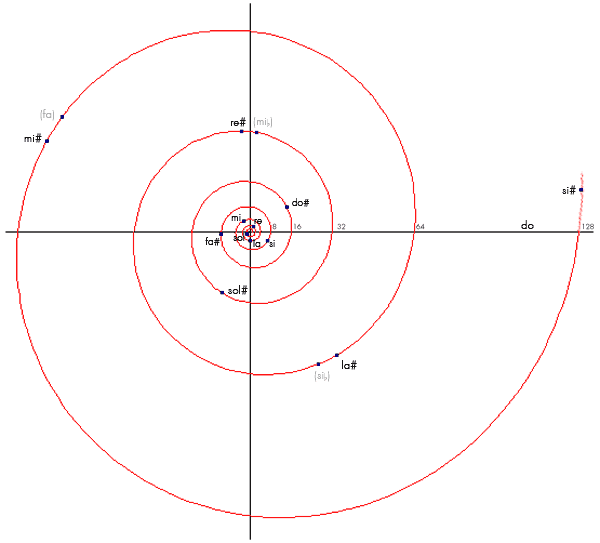
También podéis apreciar las diferencias de afinación en este gráfico extraído de la wikipedia, aunque con algunos errores corregidos del original. Los puntos negros son temperados y los azules pitagóricos. El cent es una medida de afinación equivalente a la centésima parte (logarítmica, claro está) de un semitono temperado:

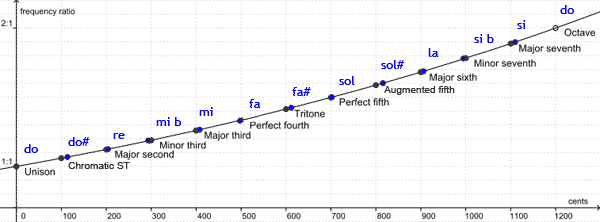
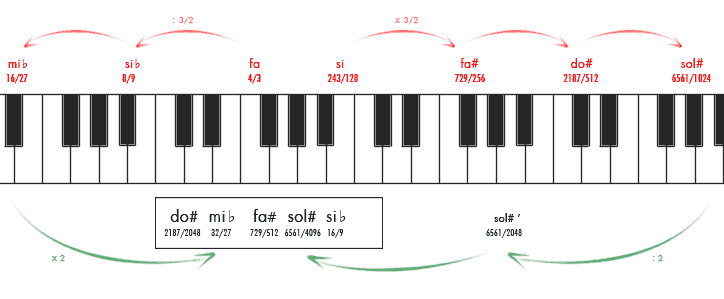
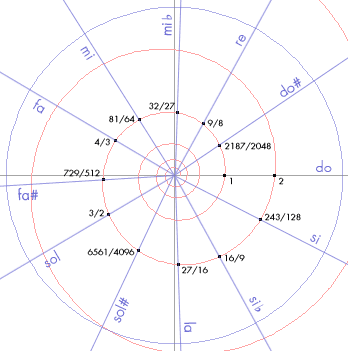
Como podéis ver, ambos sistemas son muy parecidos. Las mayores diferencias se encuentran entre las notas alteradas, especialmente al llegar al sol# (extremo del círculo de 5^as). Sin embargo, si escuchamos la escala diatónica de los sonidos naturales, afinada según el sistema pitagórico o el temperado, resultan casi indistinguibles.

La 5ª Justa:

la 5ªJ temperada es casi idéntica a la pitagórica: difieren aproximadamente 2 cents. Para que os hagáis una idea, podéis escuchar cómo suenan dos sonidos que difieren en 1 cent, 6 ó 10 en esta página de la wikipedia. Son indistinguibles.

La diferencia entre ambas 5^as recibe el nombre de schisma. Para calcular cuánto mide basta dividir la 5ª pitagórica entre la temperada, o bien, repartir la coma pitagórica entre las 12 quintas que cierran el círculo en el sistema temperado. El resultado es el mismo:

La 3ª Mayor.

La 3ªM difiere algo más entre un sistema y otro, pero sigue siendo claramente disonante en ambos. Hasta no oírlo, yo no imaginaba cuanto, así que aquí tenéis el intervalo afinado en ambos sistemas y una 3ªM consonante para compararlos.

Para escuchar más posibles comparaciones, resulta muy útil el programa Scala del que nos habló Zarlino y cuya recomendación yo reitero.

Supongamos una melodía compuesta con las notas de la escala diatónica. Cada nota tendrá una altura (una frecuencia) determinada y, al unir esas alturas, obtendremos el contorno melódico que la caracteriza. Supongamos que esa melodía ha sido compuesta para una soprano, por lo que es bastante aguda. Bien, ahora, imaginemos que tenemos una contraalto, con la voz más grave que Carmen de Mairena, empeñada en cantar esta misma melodía. Tenemos dos opciones: bien dejarla dar gallos para poner a prueba nuestra resistencia a la tortura, o bien, transportar la melodía: es decir, coger su contorno (el patrón de frecuencias característico) y hacer que empiece en una nota más grave.

Esto, en teoría, debería ser bastante fácil. En la antigüedad no se andaban con remilgos y, en lugar de transportar la melodía, transportaban toda la escala sobre la que estaba construida. Así, una nota cualquiera como «do» podía tener una frecuencia de 500 Hz un día, y 635 Hz, al otro. Sin embargo, cuando aparecían en escena instrumentos de afinación fija (como un órgano o un clave), esa aleatoriedad se volvía imposible. Al estar la escala «fija», la única solución era transportar la melodía (hacer que empezase en otra nota de la misma escala) y ahí es donde aparecía el problema: en la escala heptatónica se alternan tonos y semitonos en un orden determinado. Para repetir ese patrón desde otro punto de la escala, es necesario añadir semitonos intermedios entre ciertos tonos (he aquí el origen de las notas alteradas), pero además, es necesario que todos estos semitonos sean iguales, lo que no sucede en el sistema pitagórico.

En música, existen dos tipos de notas alteradas: los bemoles (♭), que son notas «bajadas» medio tono, y los sostenidos (#), notas «subidas» medio tono. Si todos los semitonos fuesen iguales, un do# debería sonar igual que un re♭, un re# igual que un mi♭, etcétera. Estas parejas de notas a las que les corresponde el mismo sonido se denominan enarmonías. Para que sean posibles, el sonido de cada alteración debe ser intermedio de las dos notas naturales adyacentes, pero, debido a la imperfección del círculo de 5^as, en el sistema pitagórico, los bemoles se aproximan más a la nota inferior y los sostenidos, a la superior. En esta entrada veremos por qué.

La quinta del lobo

Hace dos entradas, hablamos del origen de la escala heptatónica. Bastaba con enlazar varias quintas empezando por el fa y terminando en el si. Bien, más allá del fa y del si, para medir los intervalos de 5ª, no nos bastará con contar cuántas notas separan los extremos. Si así lo hiciésemos, al contar 5 notas ascendentes desde el si, volveríamos a obtener un fa y viceversa. Sin embargo, esta quinta es más pequeña de lo normal: sólo tiene 6 semitonos, mientras que las demás tienen 7. Por ello recibe el nombre de 5ª disminuida. El sistema pitagórico se basa en la 5ªJusta de 7 semitonos (podemos observar que el sistema es coherente: con 12 quintas de 7 semitonos, igualamos 7 octavas de 12 semitonos). Así, para subir una 5ªJ desde el si, tendremos que llegar hasta el fa# y, para bajar una desde el fa, usaremos el si♭.

Recordemos ahora que 12 quintas bien afinadas son un poquito más de 7 octavas. Si queremos cerrar el círculo en este punto, una de las quintas tendrá que medir un poquito menos que el resto (una coma pitagórica menos), no será perfectamente consonante y sonará bastante mal. Por ello, era conocida como quinta del lobo y se procuró situarla entre dos sonidos que no se empleasen habitualmente, lo más alejados posible de la escala natural. El oscuro rincón elegido fue entre el el sol# y el mi♭ que se tomaron como los extremos del círculo de quintas. Así, para afinar los semitonos entre el la-si y el re-mi, se optó por descender dos quintas a partir del fa natural, obteniendo así si♭ y mi♭. Los sonidos fa#, sol# y do# se consiguen al subir 3 quintas desde el si.

Esto significaba que, en los instrumentos de afinación fija que utilizaban este sistema, el la♭, (, afinado como un sol#, ), o el re#, (, afinado como un mi♭, ), podían sonar bastante mal, por lo que no convenía alejarse mucho de las tonalidades más cercanas a la escala natural. Podéis apreciarlo en la espiral logarítmica de la semana pasada.

Semitonos cromáticos y diatónicos

En este gráfico tenéis la misma espiral con las frecuencias de la escala cromática, pero esta vez, dado que cada 360º se repite el mismo sonido, he unido cada nota con el origen. Así, podemos ver todos los sonidos en una misma octava y observar más fácilmente los ángulos que las separan (representativos de los intervalos correspondientes). Aunque pueda parecerlo, los 12 ángulos de la imagen (12 semitonos), no son exactamente iguales: hay cinco de mayor tamaño (semitonos cromáticos) y 7 más pequeños (diatónicos).

Los semitonos cromáticos son los que hay entre notas con el mismo nombre, una natural y otra alterada, esto es, entre: do-do#, mi♭-mi, fa-fa#, sol-sol# y si♭-si. Todas estas notas se hayan en proporción de . En la imagen podéis apreciar que los ángulos son claramente mayores que los correspondientes a los semitonos diatónicos (semitonos entre notas con distinto nombre): do#-re, re-mi♭, mi-fa, fa#-sol, sol#-la, la-si♭ y si-do. La proporción en este caso es de . La diferencia, de nuevo, no es mucha: exactamente de una coma pitagórica:

Todo esto los violinistas lo saben bien, pues, a pesar de que este sistema de afinación ya no se utiliza, suele sonar mejor una nota sostenida (como fa#, sensible) que resuelve ascendentemente (sol), si ambos sonidos  están más próximos, como separados por un semitono diatónico. Por eso, quizás lleguéis a escucharles decir que las enarmonías no son posibles, que un sol♭ no es lo mismo que un fa# y demás, pero siempre en boca de la cuerda frotada: un pianista se partiría el culo.

Por último, podéis comprobar por qué la 5ª del lobo es más pequeña que el resto: mientras todas las demás tienen 3 semitonos cromáticos y 4 diatónicos, el intervalo entre mi♭ y sol#, tiene 2 semitonos cromáticos y 5 diatónicos. La diferencia es, por tanto, la prevista: una coma pitagórica.

Nota para músicos

Supongo que muchos ya habréis caído en la cuenta al leer estas entradas: el origen de la escala heptatónica explica también el orden de las tonalidades y de las alteraciones en la armadura de clave. Sol Mayor, por ejemplo, necesita solo un sostenido, pues al estar una 5ª por encima de do, utiliza los mismos intervalos para construir su escala y únicamente «se sale» de los sonidos naturales en la última 5ª,  de si a fa#.

A petición de Zarlino en el post anterior, he creado con MATLAB unas muestras de sonido para ilustrar cómo suenan los intervalos que os indicaba el otro día en gráficas de sumas de cosenos. Recordemos que habíamos llegado a dos conclusiones:

1. La disonancia está asociada a la presencia de una envolvente en la suma de los sonidos implicados en el intervalo, y esto se traduce en una sensación auditiva de «batidos».
2. Estos «batidos» son más fuertes cuanto más próximos en frecuencia están los sonidos, en consecuencia, la sensación de disonancia será mayor cuanto menor sea el intervalo.

He aquí los ejemplos de audio:

Primero quiero pedir disculpas por la última muestra, porque la mezcla de armónicos que he hecho ha quedado un poco dura (aunque en esto tiene mucho que ver el ataque, algún día os contaré…). Y segundo, comentar que estoy hablando todo el tiempo de consonancia perceptiva (término acuñado por Deutsch, 1982)^[1], directamente relacionada con la proximidad de frecuencias y presencia de estos batidos (Helmholtz, 1863)^[2], y base de la consonancia musical. La primera constituye un concepto puramente físico y fisiológico, mientras que en la segunda influyen aspectos culturales e históricos.

Ahora hablaremos de vuestra sorpresa, la sorpresa que supongo os habrá producido escuchar la quinta muestra, porque probablemente a la mayoría de vosotros os habrá resultado más desagradable, más disonante, la cuarta muestra que la quinta. ¿No decíamos que a mayor proximidad, mayor disonancia? Eso es cierto, pero hasta ahí ha llegado únicamente nuestra teoría física sobre la consonancia: todavía no hemos tenido en cuenta nuestra fisiología, nuestro oído.

Y es que nuestro sistema auditivo es un sistema real, por tanto no ideal, con ciertas limitaciones. Podemos modelar nuestro oído como un banco de filtros que proporcionan cierta respuesta en frecuencia. En concreto, la culpable de esta respuesta es la membrana basilar, situada en la cóclea. Se trata de una membrana que se encarga de separar las frecuencias que componen el sonido para que cada una de estas frecuencias sea detectada por un grupo de células destinadas a tal efecto. Para separarlas, la membrana basilar varía en masa y rigidez a lo largo de su longitud, es decir, varía su frecuencia de resonancia y de esta manera en cada trocito vibra una sola frecuencia y las demás son atenuadas. Esto limita la resolución frecuencial del oído humano. Es decir, si hay dos tonos demasiado próximos en frecuencia, nuestro cerebro no los distingue bien y por lo tanto la sensación de disonancia es menor.

Aquí entra el concepto de banda crítica^[3], que técnicamente se define como el ancho de banda de ruido alrededor de una frecuencia que es efectivo en el enmascaramiento de la misma. Coloquialmente, diremos que, dada una frecuencia, existe una porción de frecuencias alrededor de la misma en la que nos es complicado distinguir dos tonos porque están demasiado próximos, es decir, la porción de frecuencias que activan la misma zona de la membrana. Lógicamente, un oído entrenado es más capaz de discriminar tonos y por lo tanto a los músicos la quinta muestra de sonido nos suena a rayos, mientras que a otros les parecerá que suena un solo tono.

La siguiente gráfica ilustra muy bien la consonancia perceptiva en función de la porción del ancho de banda crítico que abarca el intervalo. Vemos que nuestras predicciones iniciales se cumplen a partir de 0.3, pero que también aparecen estos efectos no ideales en el origen, donde la consonancia vuelve a aumentar conforme la diferencia frecuencial tiende a cero.

Así pues, las limitaciones de nuestro sistema auditivo hacen que, para una persona con un oído medio, la máxima disonancia perceptiva se sitúe en torno al semitono. Esto varía, puesto que el ancho de banda crítico también varía con la frecuencia. La siguiente gráfica ilustra la posición de la máxima disonancia a distintas frecuencias base:

^[1] The Psychology of Music, D. Deutsch, 1982.
^[2] On the Sensations of Tone as a Physiological Basis for the Theory of Music, H. Helmholtz, 1863.
^[3] Tonal Consonance and Critical Bandwidth, R. Plomp y J. R. Levelt, 1965.

Cada octava, en el sistema musical occidental, está dividida en 12 semitonos que juntos forman la escala cromática. Estos son los 12 sonidos básicos con los que está escrita el 90% de la música que conocemos y solemos escuchar, desde el medievo hasta nuestros días. El sistema no lo inventó pitágoras: surgió en Europa en la Baja Edad Media. Sin embargo, es consecuencia de la idea de afinar los intervalos por quintas, de ahí que sigamos hablando de afinación pitagórica. La división en 12 sonidos, por tanto, no es una cuestión trivial ni arbitraria: parte de una base previa, con sus ventajas e inconvenientes.

Muchos músicos a lo largo de toda la historia han propuesto sistemas diferentes, con una octava dividida en más sonidos. Prueba de ello son los teclados de instrumentos antiguos, muchos del Renacimiento (la época dorada de la música instrumental), que pueden llegar a tener hasta 31 teclas por octava (podéis encontrar más fotos aquí o pinchando sobre la imagen), o las teorías de músicos contemporáneos interesados en el microtonalismo (Rodion Romanov nos habló en un comentario de sonido 13, por ejemplo, donde proponen un sistema de 96 sonidos por octava, pero hay muchos más).

El círculo de 5^as

La semana pasada vimos que los sonidos de la escala natural se obtenían sumando quintas desde un sonido de partida dado (en nuestro ejemplo, el do). Si continuásemos haciéndolo hasta completar 12 quintas obtendríamos los 5 sonidos que nos faltaban: las notas alteradas (las teclas negras). Sin embargo: ¿por qué pararse en el sonido número 12? Bien, la respuesta es que al subir 12 quintas, volvemos a obtener el sonido original, solo que 7 octavas más arriba. El sonido original… más o menos, de hecho, más bien menos que más y es que, como imaginaréis, por más que multipliquemos 3/2 a la enésima potencia nunca obtendremos, exactamente, una potencia de 2 y por tanto, nunca volveremos a oír exactamente el sonido del que partimos. Por ello, con este tipo de afinación el círculo de quintas no es tal: nunca llega a cerrarse. Se parece más a una espiral que podríamos prolongar hasta el infinito, obteniendo siempre sonidos intermedios de los que ya tenemos. Y aquí es donde nace la discrepancia: la espiral, en efecto, puede forzarse para quedar cerrada en el sonido número 12. A fin de cuentas, el sonido número 13 se hallaría a relativamente poca distancia del punto de partida y nuestra capacidad de discernir es limitada. Pero esta solución no es la única, según muchos tampoco la mejor y desde luego, tiene sus desventajas. Para entender la polémica pasaremos a analizar lo imperfecto que, de hecho, es el «círculo de quintas».

12 quintas no son 7 octavas

No, no lo son. Podéis comprobarlo con una calculadora: . De hecho, la diferencia parece bastante significativa. Sin embargo, debemos recordar que en música las «distancias» se perciben como proporciones. Si realizamos esta operación, vemos que el resultado es bastante parecido a 1: . Este intervalo se conoce como coma pitagórica y es menos de un octavo de tono.

En esta gráfica podéis ver una espiral logarítmica donde la frecuencia de cada sonido viene representada: . De este modo, cada vez que el ángulo se hace ó , obtenemos una nueva potencia de 2, esto es, volvemos a oír un do.

En este tipo de gráfica los intervalos vienen dados por ángulos: a ángulos iguales, intervalos iguales. El intervalo de 8ª, vendría representado por un ángulo de 2π. Para calcular el ángulo correspondiente a otra frecuencia o intervalo, invertiremos la fórmula anterior: . Así podemos hallar también el ángulo correspondiente a una 5ª: . O el ángulo correspondiente a la coma pitagórica (esto es: la distancia entre el re# y el mi♭, o entre el si# y el do), bastante pequeño en comparación: .

Este pequeño error, no obstante, supone bastantes inconvenientes de cara al desarrollo posterior de la música tonal. Por ello, el sistema de afinación pitagórico terminó siendo rechazado en pro del sistema temperado que utilizamos actualmente. En la próxima entrada veremos cuáles son estos inconvenientes.

En entradas previas de Música y matemáticas, hablábamos de la base matemática de la consonancia musical, en contraposición a la disonancia. Pero para entender el porqué oculto tras esos números, me parece necesario vislumbrar qué ocurre a nivel físico para luego intentar darle una interpretación fisiológica al fenómeno de la consonancia. Por ello, esta entrada y la próxima tocarán conceptos algo más complejos, más ingenieriles también; intentaré hacerlos accesibles y que no se me vayan de las manos, aunque no prometo nada. Hablaré de lo que sucede en el aire, de cómo vibra este, de la evolución del sonido en el tiempo. También veremos qué sucede en el ámbito más abstracto de la frecuencia, y esto nos llevará inevitablemente a hablar de cómo funciona nuestro sistema auditivo.

Antes de empezar, debe quedar claro que los conceptos de consonancia y disonancia entrañan cierta subjetividad, puesto que han ido evolucionando con la música a lo largo de los siglos. Y digo cierta porque imperativamente subyace una base física ineludible en dichos fenómenos.

Consonancias de tonos puros en el tiempo

Esta parte será la más amena y más gráfica, accesible para todos los públicos. Vamos a ver qué evolución siguen las ondas sonoras en el tiempo, la vibración que experimentan las moléculas del aire; en concreto, vamos a visualizar qué ocurre cuando mezclamos dos sonidos. Para ello, haré simples sumas de cosenos y os enseñaré la gráfica resultante (si a alguien le preocupase la fase de estos cosenos, estaría encantado de demostrarle que ésta no influye significativamente en el resultado de la suma).

Empezaremos con algo facilito, la consonancia más simple: la 8ª. Dos tonos puros, el segundo con frecuencia doble que el primero (por ejemplo, do y el do inmediatamente superior), ¿qué aspecto tendrían? El siguiente:

Como podemos observar, tenemos una onda muy suave, que no cambia bruscamente, y muy predecible. En una primera aproximación, podríamos afirmar que un sonido resulta agradable, resulta consonante, cuando tiene una forma de onda suave, lo más próxima posible a un tono puro, a una sinusoide. ¿Qué ocurrirá con la 5ª? Recordemos, relación frecuencial de 3/2:

Efectivamente, con esta consonancia seguimos teniendo una onda suave, luego parece que la cosa funciona. Vamos con la 3ª Mayor, relación frecuencial de 5/4:

Comienza a complicarse y vemos que aparece una cierta envolvente (contorno de los máximos y mínimos, perfil ondulado en el que puede enmarcarse la gráfica), aunque sigue siendo una onda suave. Si seguimos reduciendo el intervalo, vemos que lo que ocurre es que esta envolvente se va haciendo cada vez más pronunciada. Vamos con una 2ª Mayor, una disonancia, relación frecuencial de 9/8:

Ahí tenemos claramente la envolvente. Parece ser que esta modulación que aparece en los máximos, esta pequeña montaña rusa, incomoda a nuestro oído aunque la onda siga siendo bastante suave. En el extremo de la disonancia, es decir, el par de sonidos más desagradables que percibimos se dan cuando tenemos dos sonidos iguales pero ligeramente desafinados. Por ejemplo, un la a 440 Hz y otro la a 442 Hz. Tienen esta pinta:

¿Cómo? ¿Una sinusoide? ¿Se acaba de desmontar toda nuestra teoría? No, amiguitos. Estamos viendo un zoom demasiado grande. Hagamos zoom out:

Ahora sí estamos viendo lo que nos interesa. La envolvente se ha hecho tan enorme que se ha convertido en un zumbido insoportable para nuestro oído. De ahí la disonancia horrible de dos instrumentos desafinados.

Consonancias con sonidos reales

Lo anterior está desarrollado con sumas de parejas de tonos puros, pero, obviamente, los sonidos reales son más complejos: tienen armónicos (y demás historias que algún día os contaré). Vamos pues con un ejemplo con sonidos más ajustados a la realidad. ¿Qué pinta tiene más o menos un sonido real? En el siguiente gráfico tenemos un solo sonido considerando sus componentes hasta el quinto armónico (receta propia, si se correspondiera con algún instrumento real, sería pura casualidad):

Ahora sumaré este sonido real (o casi) con su 5ª, pero la quinta también estará considerada hasta el quinto armónico. Es decir, veremos la consonancia de 5ª entre dos sonidos (casi) reales:

La gráfica es bastante más compleja que antes, es más brusca, menos suave, pero la envolvente es estable, igual que en la 5ª con tonos puros.

La conclusión que sacamos es que la envolvente de la onda tiene mucho que ver con lo agradable o desagradable que nos resulta un intervalo. Apreciamos que los intervalos que consideramos consonantes tienen una envolvente muy estable, en cambio, en las disonancias aparecen modulaciones muy fuertes de la amplitud de la onda, la envolvente se dilata cada vez más en el tiempo haciéndose más perceptible conforme más disonante resulta un intervalo.

Para otro día dejamos el análisis desde el punto de vista de la frecuencia, el cual será no menos interesante, aunque sí más abstracto.