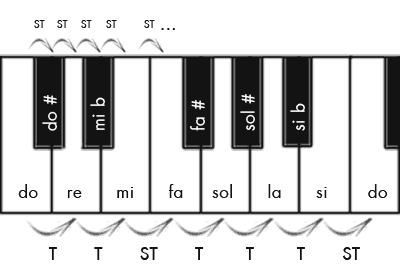
¿Alguna vez os habéis preguntado por qué son así las teclas de un piano? El teclado sigue un patrón de 7 teclas blancas entre las que se intercalan 5 negras: un total de 12 teclas por octava. Las teclas blancas corresponden a las notas de la escala natural (do, re, mi, fa, sol, la, si), las teclas negras son las notas alteradas (do#, mib, fa#, sol#, sib). Entre cada tecla y la siguiente, sea blanca o negra, hay siempre el mismo intervalo: un semitono (ST), la mitad de un tono (T). Pero entonces, ¿por qué no están todas las teclas al mismo nivel?, ¿por qué algunas notas se consideran «naturales» y otras «alteradas»?, ¿por qué los tonos y semitonos se distribuyen de esa manera y no otra en la escala natural (T, T, ST, T, T, T, ST)?, ¿por qué tiene precisamente 7 notas? (la escala pentatónica, característica de oriente, por ejemplo, sólo tiene 5). La respuesta, de nuevo, está relacionada con Pitágoras.
La afinación por 5as
El lunes os conté como la 5ª de cualquier sonido se obtiene al multiplicar su frecuencia por 3. Sin embargo, así obtenemos su quinta una octava más aguda. En rigor, tendríamos un intervalo de 12ª (una 8ª más una 5ª: como al medir los intervalos tomamos las dos notas de los extremos, las sumas en música no funcionan, siempre dan uno de más). Ese mismo sonido, una octava baja, se hallaría en una proporción de 3/2 respecto a la fundamental, y ésta es la proporción que Pitágoras tomó como base de su sistema musical.
Para reconstruir este sistema, partiremos de la nota do y supondremos, nuevamente, que su frecuencia es 1. A partir de ahí, la multiplicaremos sucesivamente por 3/2 para obtener cada nuevo sonido de la escala natural. La mayoría de estos sonidos aparecerán en escalas más agudas, pero para obtener estos sonidos en la escala original no tenemos más que bajarles una o varias veces de 8ª, esto es: dividir su frecuencia entre dos. El resultado es el que podéis ver en la siguiente imagen:
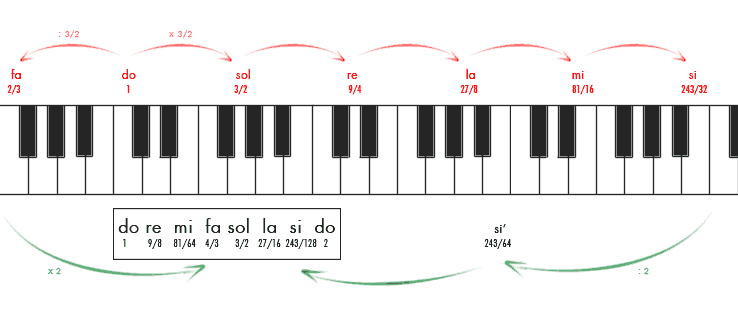Con estos datos podemos observar varias particularidades de la escala:
- Existen cinco intervalos de mayor tamaño y dos claramente más pequeños. Los intervalos más pequeños se encuentran entre el mi y el fa, y entre el si y el do agudo. Si observamos el teclado del comienzo, vemos que entre las teclas blancas correspodientes a estas notas no hay ninguna tecla negra: son los dos únicos intervalos de semitono que encontramos en la escala natural.
- La diferencia de frecuencias va aumentando según nos acercamos al agudo. No obstante, nosotros percibimos los intervalos de tono como iguales debido a que nuestra percepción es logarítmica (para intervalos iguales, donde a y b son frecuencias, se cumple que loga – logb = cte).
- Podríamos seguir añadiendo quintas obteniendo así sonidos intermedios, pero los intervalos comenzarían a ser menos homogéneos. No obstante, este es el origen de la escala cromática, como veremos el próximo día.
También podemos observar que esta escala tiene ciertos defectos o incoherencias.
- El semitono no es la mitad exacta de un tono, (256/243 ≠ √9/8). Por ello, mediante esta afinación, obtendremos dos tipos de semitonos distintos: cromáticos y diatónicos, como veremos el próximo día.
- La tercera dista mucho de ser «consonante», según la definición que dimos en un principio y la proporción que determinamos el pasado lunes (81/64 = 1,265625 ≠ 5/4 = 1,25). La tercera en esta escala resulta un poco disonante al ser mayor de lo que debería, y se la suele llamar ditono pitagórico.
Los modos griegos
Los griegos no utilizaban preferentemente la escala de do. En estas entradas la tomamos como referencia por ser la escala que se utilizó sistemáticamente en la música occidental a partir del Renacimiento (aproximadamente). Hoy la conocemos como escala diatónica Mayor. A veces se utiliza también la escala diatónica menor, que sería la escala de los sonidos naturales (las teclas blancas) solo que empezando desde la (T, ST, T, T, ST, T, T).
Los griegos, en cambio, tenían 8 escalas diferentes llamadas modos. El patrón interválico seguía siendo el mismo que el que acabamos de describir, solo que empezando desde distintos puntos de la escala. El modo más importante para los griegos, por ejemplo, era el modo dórico; la escala que va de mi a mi (ST, T, T, T, ST, T, T).
>El lunes os conté como la 5ª de cualquier sonido se obtiene al multiplicar su frecuencia por 3.
por 3/2.
Oops, no, luego lo aclaras. Sorry
Usando una escala logarítmica en el eje Y del último gráfico tendrías intervalos sobre el papel iguales a los que el oído percibe.
Eso creo que también lo aclaro. Precisamente para eso he elegido este otro tipo de escala: si de entrada utilizo una logarítmica parecería que me la he sacado de la manga. Aunque, por otra parte, se percibiría mejor que el semitono pitagórico no «mide» la mitad exacta de un tono…
Tremendo… estos post son la caña! Gracias!
[…] explicación teórica para esto que acabáis de escuchar en sus interesantísimos artículos sobre afinación y escalas musicales, pero a mí me da en las narices que si Pitágoras levantara la cabeza… ¡Iba a haber […]
Una cuerda tensada de longitud Lo, posee su primera octava para L1= Lo / 2 ; su segunda octava en Lo/4 y así sucesivamente.
Los doce semitonos s en que dividimos el segmento Lo/2 son:
s1=0.05612*Lo; s2=0.05297*Lo; s3=0.05000*Lo
s4=0.04719*Lo; s5=0.04454*Lo; s6=0.04204*Lo
s7=0.03968*Lo; s8=0.03745*Lo; s9=0.03535*Lo
s1o=0.03337*Lo;s11=0.0315*Lo;s12=0.02973*Lo
Sumándolos obtenemos el resultado = Lo/2
[…] La semana pasada vimos que los sonidos de la escala natural se obtenían sumando quintas desde un sonido de partida dado (en nuestro ejemplo, el do). Si continuásemos haciéndolo hasta completar 12 quintas obtendríamos los 5 sonidos que nos faltaban: las notas alteradas (las teclas negras). Sin embargo: ¿por qué pararse en el sonido número 12? Bien, la respuesta es que al subir 12 quintas, volvemos a obtener el sonido original, solo que 7 octavas más arriba. El sonido original… más o menos, de hecho, más bien menos que más y es que, como imaginaréis, por más que multipliquemos 3/2 a la enésima potencia nunca obtendremos, exactamente, una potencia de 2 y por tanto, nunca volveremos a oír exactamente el sonido del que partimos. Por ello, con este tipo de afinación el círculo de quintas no es tal: nunca llega a cerrarse. Se parece más a una espiral que podríamos prolongar hasta el infinito, obteniendo siempre sonidos intermedios de los que ya tenemos. Y aquí es donde nace la discrepancia: la espiral, en efecto, puede forzarse para quedar cerrada en el sonido número 12. A fin de cuentas, el sonido número 13 se hallaría a relativamente poca distancia del punto de partida y nuestra capacidad de discernir es limitada. Pero esta solución no es la única, según muchos tampoco la mejor y desde luego, tiene sus desventajas. Para entender la polémica pasaremos a analizar lo imperfecto que, de hecho, es el “círculo de quintas”. […]
Un divertido video sobre la pentatónica.
Gracias por esta serie de posts, me estoy divirtiendo de lo lindo.
Saludos
¡Qué guapo el vídeo! Gracias por la recomendación. Me cuesta creer que de verdad no estuviese preparado, pero es posible… Bobby McFerrin interactúa muchas veces con su público con resultados impresionantes.
[…] dos entradas, hablamos del origen de la escala heptatónica. Bastaba con enlazar varias quintas empezando por el fa y terminando en el si. Bien, más allá del […]
[…] publicaron dos entradas muy didácticas sobre música y matemáticas: Música y matemáticas. La afinación pitagórica. El origen de la escala h… y Música y matemáticas. Los intervalos […]
Apreciada Almudena;
Algún día iba a pasar: después de calcular los modos de vibración de cuerdas y tubos vibrantes alguien preguntó » ¿y la música es parte de la física?». Un no rotundo fue insuficiente y como siempre una pregunta lleva a otra, terminamos por indagar desde cómo consiguieron sus nombres las notas musicales hasta cómo construir una escala de Blues. Y en este viaje tu compañia fue clave mayor…
[…] Música y matemáticas. La afinación pitagórica. El origen de la escala heptatónica […]
[…] Música y matemáticas. La afinación pitagórica. El origen de la escala heptatónica. […]
La escala de mi a mi no se llama dorica sino frigica. La escala Dorica es de re a re con el siguiente orden: T,ST,T,T,T,ST,T
@Flavia:
Eso es así en los modos medievales, no en los modos griegos. Puedes consultarlo en esta página.
El módo dórico griego va de mi a mi descendentemente.