Música y matemáticas. La afinación pitagórica. El origen de la escala cromática

Publicado el por Almudena M. Castro

Cada octava, en el sistema musical occidental, está dividida en 12 semitonos que juntos forman la escala cromática. Estos son los 12 sonidos básicos con los que está escrita el 90% de la música que conocemos y solemos escuchar, desde el medievo hasta nuestros días. El sistema no lo inventó pitágoras: surgió en Europa en la Baja Edad Media. Sin embargo, es consecuencia de la idea de afinar los intervalos por quintas, de ahí que sigamos hablando de afinación pitagórica. La división en 12 sonidos, por tanto, no es una cuestión trivial ni arbitraria: parte de una base previa, con sus ventajas e inconvenientes.

Muchos músicos a lo largo de toda la historia han propuesto sistemas diferentes, con una octava dividida en más sonidos. Prueba de ello son los teclados de instrumentos antiguos, muchos del Renacimiento (la época dorada de la música instrumental), que pueden llegar a tener hasta 31 teclas por octava (podéis encontrar más fotos aquí o pinchando sobre la imagen), o las teorías de músicos contemporáneos interesados en el microtonalismo (Rodion Romanov nos habló en un comentario de sonido 13, por ejemplo, donde proponen un sistema de 96 sonidos por octava, pero hay muchos más).

cs19phs3

El círculo de 5as

La semana pasada vimos que los sonidos de la escala natural se obtenían sumando quintas desde un sonido de partida dado (en nuestro ejemplo, el do). Si continuásemos haciéndolo hasta completar 12 quintas obtendríamos los 5 sonidos que nos faltaban: las notas alteradas (las teclas negras). Sin embargo: ¿por qué pararse en el sonido número 12? Bien, la respuesta es que al subir 12 quintas, volvemos a obtener el sonido original, solo que 7 octavas más arriba. El sonido original… más o menos, de hecho, más bien menos que más y es que, como imaginaréis, por más que multipliquemos 3/2 a la enésima potencia nunca obtendremos, exactamente, una potencia de 2 y por tanto, nunca volveremos a oír exactamente el sonido del que partimos. Por ello, con este tipo de afinación el círculo de quintas no es tal: nunca llega a cerrarse. Se parece más a una espiral que podríamos prolongar hasta el infinito, obteniendo siempre sonidos intermedios de los que ya tenemos. Y aquí es donde nace la discrepancia: la espiral, en efecto, puede forzarse para quedar cerrada en el sonido número 12. A fin de cuentas, el sonido número 13 se hallaría a relativamente poca distancia del punto de partida y nuestra capacidad de discernir es limitada. Pero esta solución no es la única, según muchos tampoco la mejor y desde luego, tiene sus desventajas. Para entender la polémica pasaremos a analizar lo imperfecto que, de hecho, es el «círculo de quintas».

12 quintas no son 7 octavas

No, no lo son. Podéis comprobarlo con una calculadora: 2^7 = 128 \ne\left( \frac{3}{2} \right)^{12} = 129.746. De hecho, la diferencia parece bastante significativa. Sin embargo, debemos recordar que en música las «distancias» se perciben como proporciones. Si realizamos esta operación, vemos que el resultado es bastante parecido a 1: \left( \frac{3}{2} \right)^{12} / 2^7 = 1.013. Este intervalo se conoce como coma pitagórica y es menos de un octavo de tono.

espiral1

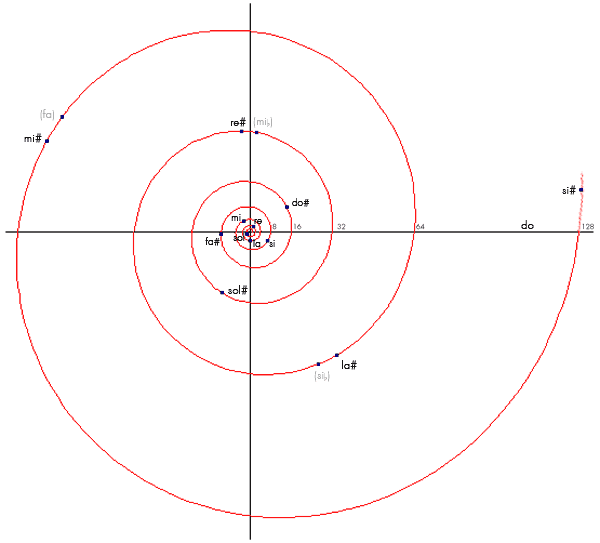
En esta gráfica podéis ver una espiral logarítmica donde la frecuencia de cada sonido viene representada: r = 2^{\theta/2 \pi}. De este modo, cada vez que el ángulo se hace 0 ó 2 \pi k, obtenemos una nueva potencia de 2, esto es, volvemos a oír un do.

En este tipo de gráfica los intervalos vienen dados por ángulos: a ángulos iguales, intervalos iguales. El intervalo de 8ª, vendría representado por un ángulo de 2π. Para calcular el ángulo correspondiente a otra frecuencia o intervalo, invertiremos la fórmula anterior: \theta = 2 \pi log_2 r. Así podemos hallar también el ángulo correspondiente a una 5ª: \theta = 2 \pi log_2 (3/2) \simeq 210.5865^o. O el ángulo correspondiente a la coma pitagórica (esto es: la distancia entre el re# y el mi♭, o entre el si# y el do), bastante pequeño en comparación: \theta = 2 \pi log_2 (3^{12}/2^{19}) \simeq 7.038^o.

Este pequeño error, no obstante, supone bastantes inconvenientes de cara al desarrollo posterior de la música tonal. Por ello, el sistema de afinación pitagórico terminó siendo rechazado en pro del sistema temperado que utilizamos actualmente. En la próxima entrada veremos cuáles son estos inconvenientes.

Entradas relacionadas:

13 comentarios sobre “Música y matemáticas. La afinación pitagórica. El origen de la escala cromática”

  3. Muy bonita la espiral, pero se puede prescindir de la componente radial y usar sólo la angular para dibujar un ‘círculo de quintas’.

  4. Ese es el siguiente paso. ¡Te adelantas siempre a mis entradas! jejeje.
    Me interesaba la espiral porque la distancia del centro a cada punto representa la frecuencia «real» de cada sonido. En cualquier caso, obtener esos ángulos es sencillo: como cada 2pi se repite la misma nota (cada 2pi se duplica la frecuencia), basta con unir cada punto con el centro. Esa gráfica está en la entrada programada para el martes.

  7. Trobo que aquesta espiral és falsa ja que entre una octava i una altra no augmenta «la distància», encara que es dupliqui la frequència, per tant aquesta represnetació gràfica falseja o dona una impressió visualment incorrecta, és com si donés a entendre que a mesura que augmenten els números, les octaves també són més grans, en conseqüència no es poden represnetar d’aquesta manera.

  8. @Joel: No sé si te he entendido bien, Joel, porque lo cierto es que no hablo catalán. En este sentido, si cometo algún error en mi interpretación, puedes corregirme en castellano, inglés, gallego, portugués o francés, que me defiendo mejor.

    En cualquier caso, en el texto viene todo explicado. La distancia al centro es representativa de la frecuencia absoluta de cada sonido. En este sentido, cada octava más aguda implica una mayor diferencia de frecuencias, ergo, una mayor «distancia». Por ejemplo la 220 Hz, la 440 Hz y la 880 Hz. La «distancia» o la diferencia de frecuencias del primero al segundo, es 220 Hz. La diferencia de frecuencias del segundo al tercero es 440 Hz.

    Como bien dices, todas las octavas, para el oído, son iguales, ya que nuestra percepción del sonido en este ámbito es logarítmica (como la espiral, por cierto). Para eso sirven los ángulos: a ángulos iguales, intervalos iguales. Pero, en este caso, es el ángulo el que representa esa igualdad. Cada octava viene representada por un ángulo de 2pi.

    No es que la representación esté mal, es que no representa lo que tú crees o lo que estabas esperando. Es como si piensas que una gráfica que relaciona la velocidad con el tiempo representa «mal» el espacio o da una visualización «incorrecta» de la aceleración. Sencillamente, estás buscando peras en una carnicería.
    En este caso, las distancias no son intervalos, son diferencias de frecuencias. Los ángulos son los intervalos.

  12. Muy buen artículo……. Excelente. Gracias por la publicación, me aclaraste bastantes dudas al respecto de la afinación. A propósito de este tema ¿conoces alguna relación entre el sistema de afinación y el número fi 1,618? La otra vez vi un documental donde supuestamente Pitágoras relacionaba fi con una escala en particular o con alguna aromía.
    Un abrazo y gracias. (Felipe de Chile)

Comentarios cerrados.