Música y matemáticas. Los intervalos consonantes

Publicado el por Almudena M. Castro

Hoy hablaremos de los principales intervalos consonantes; según los definimos el otro día: los intervalos entre sonidos cuyas frecuencias están en proporción de un número entero menor que 7. Son, por tanto, los intervalos que se obtienen al dividir una cuerda entre estos mismos números. Si tenéis una guitarra en casa, os invito a experimentar con ella.

cuerdaarmónicostecladoarmónicos

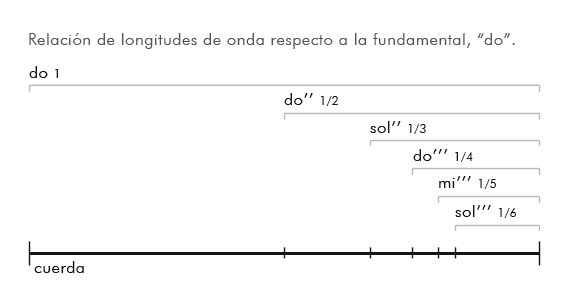
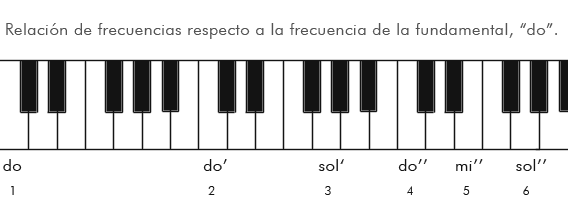
La 8ª Justa

Supongo que todos recordáis la famosa canción de sonrisas y lágrimas («do, es trato de varón»). Y, supongo que todos recordáis que, después del si «otra vez ya viene el do, do, do…». Esto, que parece trivial, denota una característica muy peculiar de nuestra audición y es que percibimos el sonido de forma cíclica o incluso circular. Este círculo se cierra cada vez que un sonido dobla su frecuencia. Es decir, si una nota determinada, pongamos, un do, tiene una frecuencia de 525 Hz, al oír un sonido con el doble de frecuencia, 1050 Hz, volvemos a reconocer «el mismo» sonido, un do, solo que esta vez, más agudo. En música este intervalo se conoce como intervalo de 8ª u 8ª Justa.

intervalos

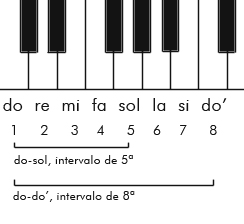
Ya mencionamos que un intervalo es la distancia que separa dos sonidos o la proporción que existe entre sus frecuencias. En música, el intervalo entre dos notas se denomina según el número de notas de la escala tradicional (do re mi fa sol la si) que las separa, incluidas las dos de los extremos. Así, el intervalo do-sol por ejemplo, sería una 5ª: 1 do, 2 re, 3 mi, 4 fa, 5 sol. El intervalo de un do al siguiente do más agudo, una 8ª: 1 do, 2 re, 3 mi, 4 fa, 5 sol, 6 la, 7 si, 8 do.

La semejanza entre dos sonidos separados por una 8ª, (esto es, dos sonidos cuyas frecuencias guardan una proporción de 2 a 1), es tal, que muchas veces no nos percatamos de que son sonidos diferentes. Por ejemplo: si se le pide a un hombre y a una mujer que canten la misma melodía, automáticamente, la mujer la cantará una 8ª más aguda que el hombre. La cantará constantemente al doble de frecuencia, pero, probablemente, no se dé ni cuenta.

Por este motivo, el otro día comentaba que los intervalos de sonidos «consonantes» son, tanto aquellos cuya proporción de frecuencias es un número entero menor que 7, como esos mismos números dividos o multiplicados por potencias de dos, ya que, cada vez que duplicamos la frecuencia de un sonido, volvemos a obtener, prácticamente, el mismo sonido. Supongamos que un do tiene frecuencia 1 y, un sol, tiene frecuencia 3 (omito las unidades pues son datos inventados y lo único que nos interesa es la proporción, no los Herzios reales). Las frecuencias 3/2, 3/4, 6 ó 12 también corresponderán a distintos soles de la escala, sumamente parecidos al sol de frecuencia 3. Tan parecidos que el intervalo do-sol resulta siempre consonante, sea cual sea el sol que tomemos.

tecladoarmónicos2

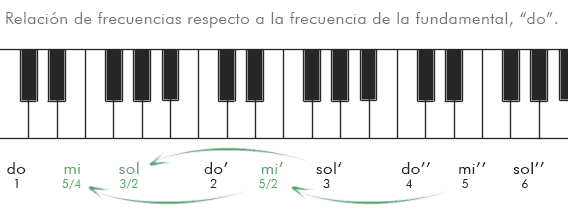
La 5ª Justa

Precisamente el siguiente intervalo consonante es el de 5ª Justa. Al duplicar la frecuencia de una nota cualquiera por dos, obtenemos la misma nota más aguda. Al triplicarla, obtenemos su 5ª (aunque en una escala más aguda). Es un intervalo fundamental, pues los griegos lo tomaron como base de su sistema musical y aún hoy sigue revelándose en la base de la armonía tonal.

La 3ª Mayor

La 3ª Mayor se obtiene al multiplicar por 5 la frecuencia fundamental. Este intervalo tardó bastante más en ser aceptado, en parte porque los griegos no le prestaron la menor atención. Sin embargo, los que sepáis algo de música, sabréis reconocer en esta interválica (fundamental, 3ª y 5ª), el acorde de triada básico en armonía tonal.

Entradas relacionadas:

17 comentarios sobre “Música y matemáticas. Los intervalos consonantes”

  1. Pues anda, gracias por la explicación. En mi rancho hubo un señor el siglo pasado que decidió reinventar esto de la escala cromática. Inventó el a href=»http://sonido13.tripod.com/»>sonido 13, todo muy bien fundamentado con matemáticas y acústica y modificó instrumentos para tocar este sonido mas cercano, según el, a la realidad matemática de la música.

  3. Como dice Rodion, todo lo que se dice aquí corresponde a los descubrimientos acústicos de los griegos.

    En instrumentos de afinación fija, como los pianos, TODOS los intervalos excepto la octava deben ser ligeramente «desafinados» para poder utilizar sólo doce teclas por octava (por ejemplo, para que una sola tecla negra pueda ser usada tanto como Re# como Mib).

    Esto es así porque los números 2 y 3 son primos entre sí.

  4. Ya. En este artículo hablamos de las consonancias «ideales», porque quiero explicar más tarde por qué se producen los fenómenos de consonancia y disonancia. Ambos tienen una explicación fisiológica.
    @Juan Ignacio: Iré explicando los distintos sistemas de afinación en orden cronológico. Hoy o mañana caerá el sistema pitagórico (basado en la 5ª Justa), después pasaré por los sucesivos sistemas medievales (hubo muchos, de hecho, algunos órganos antiguos tenían más de 12 teclas por octava, un fa# era distinto al sol b, por ejemplo), hasta llegar al sistema actual, consecuencia directa de la armonía clásica y su evolución posterior (las modulaciones a cualquier tono no serían posibles si todos los semitonos no fuesen iguales).
    Siento las imprecisiones: el hecho de mostrar un teclado es un recurso ejemplificardor que, sin duda, puede resultar confuso. En cualquier caso, agradezco tu aclaración.
    @ Rodion Romanov: Echaré un vistazo al link que nos ofreces, parece interesante. Hay algunos grupos que tampoco están conformes con el sistema de afinación actual y pretenden resucitar las viejas consonancias perfectas. Por ejemplo: existe una asociación por la defensa de la 5ª pitagórica. No deja de resultar bastante cómico…

  6. La octava ha estado reconocida como consonante, como bien dices desde la música griega, sin embargo y, al igual que la 3ª, la 5ª no empezó a ser masivamente utilizada hasta la polifonía, comenzando en los organum y desarrollándose poco a poco la armonía tonal. En la armonía modal la 4ª tenía un papel preponderante

  7. @ Sergio: ¿A qué te refieres con armonía modal? Hasta donde yo sé, la música griega era monódica. ¿O lo dices por el tetracordo? En cualquier caso, los griegos admitían 3 consonancias, a saber: 8ª, 5ª, 4ª…
    Por otra parte, según tenía entendido, la armonía de los primeros organa de la Edad Media, consistían en duplicar una melodía a un intervalo de 5ª (o 4ª), que se podía convertir en 4ª (o 5ª) si una de las dos voces era duplicada a la 8ª. A fin de cuentas, una 4ª no es más que una 5ª invertida, por lo que es raro considerar consonancia la una, desestimando la otra. La armonía de estos organa se considera modal (desde luego, no tonal), y en ella la 5ª era admitida como consonancia, junto con la 8ª y la 4ª.
    Pero vaya, si tuvieses alguna referencia que dijese lo contrario, tendría interés en leerla.

  8. De hecho, acabo de leer en otro sitio, en el organum solía duplicarse la voz principal a una cuarta descendente… lo que viene a ser la 5ª ascendente solo que una 8ª baja, y luego ambas se duplicaban otra vez a la 8ª.

  11. Creo recordar que la evolución fue así: Fund-8ª, 4ª-Fund-8ª , Fund-5ª-8ª (es lo mismo de antes) y Fund-3ªM-5ª… Este ultimo paso tardaron bastante en darlo porque, salvo en Inglaterra (no Reino Unido) las terceras no se consideraban consonantes y tampoco eran fáciles de dar con los sistemas de afinación que había entonces. En fin, toda esta historia es apasionante y espero nuevos episodios de vuestra serie.

Comentarios cerrados.