Supongamos una melodía compuesta con las notas de la escala diatónica. Cada nota tendrá una altura (una frecuencia) determinada y, al unir esas alturas, obtendremos el contorno melódico que la caracteriza. Supongamos que esa melodía ha sido compuesta para una soprano, por lo que es bastante aguda. Bien, ahora, imaginemos que tenemos una contraalto, con la voz más grave que Carmen de Mairena, empeñada en cantar esta misma melodía. Tenemos dos opciones: bien dejarla dar gallos para poner a prueba nuestra resistencia a la tortura, o bien, transportar la melodía: es decir, coger su contorno (el patrón de frecuencias característico) y hacer que empiece en una nota más grave.
Esto, en teoría, debería ser bastante fácil. En la antigüedad no se andaban con remilgos y, en lugar de transportar la melodía, transportaban toda la escala sobre la que estaba construida. Así, una nota cualquiera como «do» podía tener una frecuencia de 500 Hz un día, y 635 Hz, al otro. Sin embargo, cuando aparecían en escena instrumentos de afinación fija (como un órgano o un clave), esa aleatoriedad se volvía imposible. Al estar la escala «fija», la única solución era transportar la melodía (hacer que empezase en otra nota de la misma escala) y ahí es donde aparecía el problema: en la escala heptatónica se alternan tonos y semitonos en un orden determinado. Para repetir ese patrón desde otro punto de la escala, es necesario añadir semitonos intermedios entre ciertos tonos (he aquí el origen de las notas alteradas), pero además, es necesario que todos estos semitonos sean iguales, lo que no sucede en el sistema pitagórico.
En música, existen dos tipos de notas alteradas: los bemoles (♭), que son notas «bajadas» medio tono, y los sostenidos (#), notas «subidas» medio tono. Si todos los semitonos fuesen iguales, un do# debería sonar igual que un re♭, un re# igual que un mi♭, etcétera. Estas parejas de notas a las que les corresponde el mismo sonido se denominan enarmonías. Para que sean posibles, el sonido de cada alteración debe ser intermedio de las dos notas naturales adyacentes, pero, debido a la imperfección del círculo de 5as, en el sistema pitagórico, los bemoles se aproximan más a la nota inferior y los sostenidos, a la superior. En esta entrada veremos por qué.
La quinta del lobo
Hace dos entradas, hablamos del origen de la escala heptatónica. Bastaba con enlazar varias quintas empezando por el fa y terminando en el si. Bien, más allá del fa y del si, para medir los intervalos de 5ª, no nos bastará con contar cuántas notas separan los extremos. Si así lo hiciésemos, al contar 5 notas ascendentes desde el si, volveríamos a obtener un fa y viceversa. Sin embargo, esta quinta es más pequeña de lo normal: sólo tiene 6 semitonos, mientras que las demás tienen 7. Por ello recibe el nombre de 5ª disminuida. El sistema pitagórico se basa en la 5ªJusta de 7 semitonos (podemos observar que el sistema es coherente: con 12 quintas de 7 semitonos, igualamos 7 octavas de 12 semitonos). Así, para subir una 5ªJ desde el si, tendremos que llegar hasta el fa# y, para bajar una desde el fa, usaremos el si♭.
Recordemos ahora que 12 quintas bien afinadas son un poquito más de 7 octavas. Si queremos cerrar el círculo en este punto, una de las quintas tendrá que medir un poquito menos que el resto (una coma pitagórica menos), no será perfectamente consonante y sonará bastante mal. Por ello, era conocida como quinta del lobo y se procuró situarla entre dos sonidos que no se empleasen habitualmente, lo más alejados posible de la escala natural. El oscuro rincón elegido fue entre el el sol# y el mi♭ que se tomaron como los extremos del círculo de quintas. Así, para afinar los semitonos entre el la-si y el re-mi, se optó por descender dos quintas a partir del fa natural, obteniendo así si♭ y mi♭. Los sonidos fa#, sol# y do# se consiguen al subir 3 quintas desde el si.
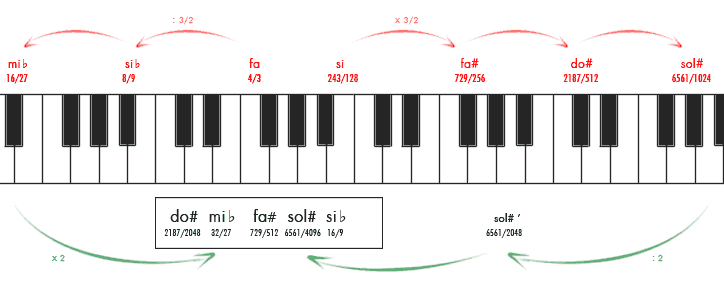
Esto significaba que, en los instrumentos de afinación fija que utilizaban este sistema, el la♭, (
Semitonos cromáticos y diatónicos
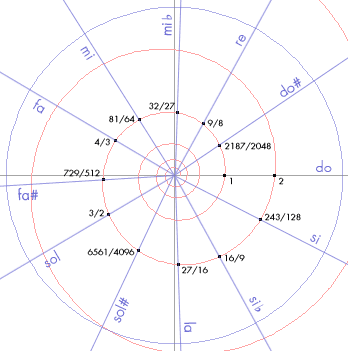
En este gráfico tenéis la misma espiral con las frecuencias de la escala cromática, pero esta vez, dado que cada 360º se repite el mismo sonido, he unido cada nota con el origen. Así, podemos ver todos los sonidos en una misma octava y observar más fácilmente los ángulos que las separan (representativos de los intervalos correspondientes). Aunque pueda parecerlo, los 12 ángulos de la imagen (12 semitonos), no son exactamente iguales: hay cinco de mayor tamaño (semitonos cromáticos) y 7 más pequeños (diatónicos).
Los semitonos cromáticos son los que hay entre notas con el mismo nombre, una natural y otra alterada, esto es, entre: do-do#, mi♭-mi, fa-fa#, sol-sol# y si♭-si. Todas estas notas se hayan en proporción de 
Todo esto los violinistas lo saben bien, pues, a pesar de que este sistema de afinación ya no se utiliza, suele sonar mejor una nota sostenida (como fa#, sensible) que resuelve ascendentemente (sol), si ambos sonidos están más próximos, como separados por un semitono diatónico. Por eso, quizás lleguéis a escucharles decir que las enarmonías no son posibles, que un sol♭ no es lo mismo que un fa# y demás, pero siempre en boca de la cuerda frotada: un pianista se partiría el culo.
Por último, podéis comprobar por qué la 5ª del lobo es más pequeña que el resto: mientras todas las demás tienen 3 semitonos cromáticos y 4 diatónicos, el intervalo entre mi♭ y sol#, tiene 2 semitonos cromáticos y 5 diatónicos. La diferencia es, por tanto, la prevista: una coma pitagórica.
Nota para músicos
Supongo que muchos ya habréis caído en la cuenta al leer estas entradas: el origen de la escala heptatónica explica también el orden de las tonalidades y de las alteraciones en la armadura de clave. Sol Mayor, por ejemplo, necesita solo un sostenido, pues al estar una 5ª por encima de do, utiliza los mismos intervalos para construir su escala y únicamente «se sale» de los sonidos naturales en la última 5ª, de si a fa#.
Que maravilla de entradas. He de reconocer que por allí del (2187/2048)/(256/243) ya estaba mas que perdido, pero me maravilla la percepción natural que tenemos de fenómenos físicos, por un lado. Es decir no necesitamos saber de quintas ni terceras para chiflar una cancioncilla cualquier día mas o menos soleado. Está en nuestro hardware :D.
Por el otro lado la manera de profundizar (complicar ?) lo que vamos comprendiendo. Gracias, Almudena.
Estoy de acuerdo con Rodion la serie de entradas me encanta aunque a veces sean un poco complicadas de entender. Seguid así.
1/4 de talibán ortográfico para Almudena en el último párrafo «Nota para músicos», 1/8 de «gallifante» para el que lo encuentre.
Un saludo afectuoso.
Me sumo a las enhorabuenas!
Para desengrasar un poco os recomiendo que veáis el fantástico video http://www
en el que Bobby Mc Ferrin habla de la omnipresente escala pentatónica Fa-Do-Sol-Re-La (o lo que es lo mismo, las teclas negras). Eso es hacer divulgación!
Muchas gracias, me alegra que os gusten. Es un tema que me apasiona, aunque ciertamente explicarlo puede resultar complejo. Se trata de resumir muchos conceptos que requieren quizás mucho más tiempo de asimilación… En cualquier caso, supongo que lo más díficil de entender son los conceptos musicales más que los matemáticos ¿no? Me interesa esta cuestión.
@José Luis: Confieso que me he quedado un poco bizca buscando la falta. Se me ocurre que pueda ser: la coma que sobraba en la segunda línea del párrafo (ya corregida) o el adverbio «solo», sin acento, que, de todos modos, no creo que deba llevarlo pues resultaría difícil confundirlo con un adjetivo. Si no es eso ¡necesito alguna pista!
@Zarlino: Es genial el vídeo, hace unos días otro lector lo recomendó también por aquí e inmediatamente lo publicaron Maikel Nai y Microsiervos. Resulta increíble que la actuación no estuviese preparada.
Por lo que sé, la escala pentatónica (la más conocida) es anterior a la heptatónica de Pitágoras, pero está basada en el mismo principio: para obtenerla basta acortar el círculo de quintas antes de llegar al Mi y al Si.
@Almudena:
Efectivamente me refería a la tilde del «sólo», yo creía que la debía llevar ya que se puede cambiar por solamente pero parece que no es obligatoria como tu bien dices.
http://www.ocordero.com/articulos/solo.htm
Sólo espero escuchar solo un solo tuyo al piano. ;-)
El vídeo de zarlino una gozada, gracias.
Un saludo
En algún sitio leí que todas las civilizaciones, por primitivas que sean, tienen una escala pentatónica y —como McFerrin muestra— parece ser consustancial a nuestra percepción de la música. Por lo visto, ae han encontrado flautas prehistóricas de la edad de piedra (hechas con huesos, no con piedras) afinadas con esa escala.
Por otra parte, si se quiere cerrar el círculo de quintas con cinco saltos el último debe ser apreciablemente más corto que una quinta justa… digamos que más que una ‘quinta del lobo’ es una ‘quinta de del diplodocus’ o algo así!
La verdad es que no lo sé, no estoy versada en historia de la música oriental. Te digo lo que he leído en más de un sitio, pero tampoco sé si estas fuentes son de fiar. En cualquier caso, no es necesario que el círculo se cierre. En la heptatónica tampoco se cierra. La necesidad de un «círculo» cerrado con intervalos iguales aparece con la necesidad de realizar modulaciones y transportes en música y, si no me equivoco esto no sucede hasta la Baja Edad Media.
Por otra parte, lo que dices es perfectamente posible. Cuando Kodaly investigó el folklore de su tierra para idear un sistema pedagógico «natural» (esto es, que a los niños no les costase entonar las canciones y lo hicieran «instintivamente»), descubrió que en las canciones infantiles el intervalo más elemental era una 3ª menor mi-sol. Después añadió un la y luego, creo (debo comprobarlo), un re y un do. Esto es: también Kodaly pensó que la escala pentatónica era la óptima para enseñar música a aquellos que aún no han adquirido una cultura musical. O bien, pensó que los semitonos de la heptatónica serían difíciles de afinar para los infantes… ni idea.
De todos modos, que sea una escala más o menos intuitiva no invalida que luego los chinos, al teorizar sobre ella, se basasen en el intervalo de 5ª. Habrá que investigarlo.
[…] (8as y 5as), la incompatibilidad entre ambas daba lugar a bastantes inconvenientes, tal como vimos la semana pasada. Como alternativa se propusieron otros sistemas a lo largo de la historia, algunos basados en la […]
M’agradaria fer un apreciació molt important respecte a l’anomenada quinta de l llop, ja que no he trobat enlloc la justa resposta. A tot arreu se li diu «quinta» del llop. Alguns n’anomenen interval «residual» , clar, residual si es mira des del punt de vista del temperament igual, però no. Ni és quinta del llop ni és interval residual. En el sistema pitagòric cada so te la seva representació per tant l’anomenada quinta del llop no és una quinta ni un interval residual sinó una SEXTA DISMINUIDA, que si en un moment cal interpreta, s’interpreta i ja està. Una cosa molt diferent és que aquest interval faci nosa a l’hora de «tancar el cercle» i es vulgui igualar una sexta disminuïda amb una quinta. conceptualment, és un error.
Pero es que, de hecho, en armonía tonal se da por válida la enarmonía.
El hecho de que tal, sea ficticia, es el motivo por el que, en ciertos periodos de la historia donde todavía se funcionaba con afinación pitagórica, hiciesenn falta teclados con 32 teclas por octava (se negaban a «cerrar el círculo» a la fuerza).
Como tal cosa resulta poco práctica, finalmente, se acotó el número de sonidos por octava a 12. En efecto, esto es una ficción, una mentirijilla. Pero es una ficción que ha dado lugar a toda la música que conocemos a partir del periodo barroco y el clasicismo.
La asimilación de una 6ª disminuida a una 5ª, sin duda, responde a esta ficción llamada armonía. Pero es una ficción aceptada y, a estas alturas, insustituíble.
Almudena, totalment d’acord, de fet ja des del principi hi he estat d’acord, simplement no estic d’acord que no parlin de 6ª disminuïda. Estic 100% d’acord amb el temperament uniforme, sense el qual no podriem modular per exemple DoM-MiM-do#m-DO#M=R3bM= II> (sexta napolitana) de DOM, només per posar un exemple entre molts. En altres paraules: els avantatges del temperament uniforme són superiors als avantatges del sistema pitagòric o de Zarlino, especialment en intruments de teclat o sons fixos.
Un altre avatange que té el temperament uniforme, al meu entendre, és l’ambiguitat. Si l’ambiguitat, perquè un acord enharmònic com p. ex. la 7ª de dominant = acord de 6ª augmentada, en sistema pitagòric tindria de ben segur una sonoritat diferent la qual cosa faria endevinar a una oïda entrenada la seva direccionalitat resolutiva, mentre que en el sistema temperat no endevines cap on anirà l’acord fins que no apareix l’acord sobre el qual resol. És a dir:la limitació a 12 sons queda sobradament compensada
P.S Almudena, m’ha agradat molt trobar un llloc com aquest on es parli d’aquests temes, per cert, no gaire assidus, ni tan sols entre músics.
Almudena, en relació al meu comentari sobre l’espiral logaritmica que he fet: no cal que m’ho expliquis perquè jo també sóc músic i ja sé que una octava és el doble de freqüència. Perquè m’entenguis: al meu entedre trobo totalment correcte l’espiral q
@Joel: Sería un detalle por tu parte hacer un esfuerzo para entendernos y contestar en castellano.
oblida aquest darrer comentari se m’ha col·locat per error
ah i et felicito per entendre tan bé el català. Jo pensava que hvies utilitzat el traductor de google.