Por qué correr bajo la lluvia SÍ merece la pena

Publicado el por Almudena M. Castro

Hace unos días, en Ya está el listo que todo lo sabe apareció publicado un post según el cual un hombre caminando lentamente bajo la lluvia se mojaría menos que uno que avanzase a gran velocidad para recorrer una distancia dada. La verdad es que no era la primera vez que me planteaba esta cuestión y siempre había llegado a la conclusión contraria (por métodos no muy rigurosos, eso sí). Así que este fin de semana me he puesto a pensar (¡ooooooh!) y el resultado es la disertación físico-matemática que podéis leer más abajo. El trabajo de escribirla en forma de post no ha sido menos arduo: Iñaki lleva desde el sábado pasando formulitas a \LaTeX, traduciéndolo todo a un lenguaje más «científico», y sobre todo, escuchando mis paranoias sobre tormentas y demás. Dios se lo pague con una buena novia.

Análisis matemático

Vamos a considerar que el hombre es un ladrillo para simplificar. Por lo tanto, tenemos que considerar lo que se moja la superficie de la cabeza y la superficie frontal del cuerpo. Trataremos ambas situaciones por separado, pues luego basta con aplicar el principio de superposición. Asumiremos que la densidad de gotas de agua en todo el espacio es constante y que llueve de manera vertical (en ausencia de viento). La velocidad de las gotas de agua es constante. Veamos un esquema:

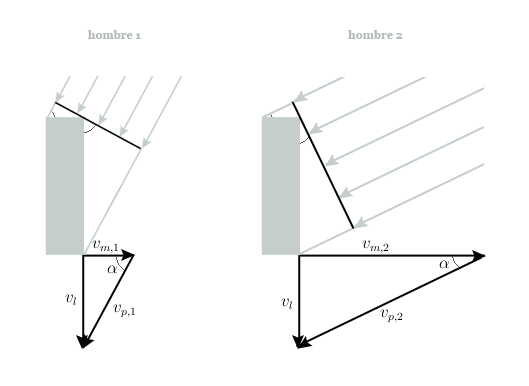
Donde:

  • v_{m,x} \equiv \mbox{velocidad del hombre } x
  • v_l \equiv \mbox{velocidad de la lluvia} \equiv \mbox{cte.}
  • v_{p,x} \equiv \mbox{velocidad de la lluvia percibida por el hombre }x
  • \alpha \equiv \acute a \mbox{ngulo de la superficie perpendicular a la velocidad percibida}

Realizamos las siguientes definiciones:

  • \mbox{Densidad de la lluvia} \equiv \rho \equiv \mbox{cte.}
  • \mbox{Superficie del cuerpo } \equiv S_b \equiv \mbox{cte.}
  • \mbox{Superficie de la cabeza } \equiv S_h \equiv \mbox{cte.}
  • \mbox{Superficie efectiva del hombre } x \equiv S_{p,x}
  • \mbox{Cantidad de lluvia que recibe en el cuerpo el hombre } x \equiv Q_{b,x}
  • \mbox{Cantidad de lluvia que recibe en la cabeza el hombre } x \equiv Q_{h,x}
  • \mbox{Distancia hasta el refugio} \equiv s = v_m \cdot t \equiv \mbox{cte.}

Primero vamos a considerar la lluvia que recibe el cuerpo. Obtenemos la superficie efectiva que es perpendicular a la velocidad percibida de la lluvia. Sabiendo que:

\cos \alpha = \displaystyle \frac{v_{m,x}}{v_{p,x}}

Entonces:

S_{p,x} = S_b \cdot \cos \alpha = \displaystyle \frac{S_b \cdot v_{m,x}}{v_{p,x}}

Por lo tanto, la cantidad de agua recibida por el cuerpo será proporcional a la densidad de la lluvia, a la superficie efectiva, a la velocidad de la lluvia relativa al hombre (velocidad percibida) y al tiempo. Es decir:

Q_{b,x} = \rho \cdot S_{p,x} \cdot v_{p,x} \cdot t = \displaystyle \frac{\rho \cdot S_b \cdot v_{m,x} \cdot v_{p,x}}{v_{p,x}} \cdot t = \displaystyle \frac{\rho \cdot S_b \cdot v_{m,x} \cdot v_{p,x} \cdot s}{v_{p,x} \cdot v_{m,x}}

Simplificando, nos queda:

Q_{b,x} = \rho \cdot S_b \cdot s

Es decir, nos queda algo constante: la densidad de la lluvia es constante, la superficie del cuerpo es la misma para ambas situaciones y el espacio a recorrer hasta el refugio más cercano es el mismo. Nuestro cuerpo se moja igual si corremos o andamos.

En segundo lugar vamos a considerar la lluvia que recibe la cabeza. Obtenemos la superficie efectiva que es perpendicular a la velocidad percibida de la lluvia. Sabiendo que:

\sin \alpha = \displaystyle \frac{v_l}{v_{p,x}}

Entonces:

S_{p,x} = S_h \cdot \sin \alpha = \displaystyle \frac{S_h \cdot v_l}{v_{p,x}}

Por lo tanto, la cantidad de agua recibida por la cabeza será a la expresión anterior. Es decir:

Q_{h,x} = \rho \cdot S_{p,x} \cdot v_{p,x} \cdot t = \displaystyle \frac{\rho \cdot S_h \cdot v_l \cdot v_{p,x}}{v_{p,x}} \cdot t = \displaystyle \frac{\rho \cdot S_h \cdot v_l \cdot v_{p,x} \cdot s}{v_{p,x} \cdot v_{m,x}}

Simplificando, nos queda:

Q_{h,x} = \rho \cdot S_h \cdot s \cdot \displaystyle \frac{v_l}{v_{m,x}}

En esta ocasión, la densidad, la superficie de la cabeza, el espacio y la velocidad de la lluvia son constantes. Pero la cantidad de agua que recibe la cabeza también depende de la velocidad del hombre y vemos que es inversamente proporcional a ésta. Es decir, cuanto más corremos, menos se nos moja la cabeza.

Conclusiones

Cómo se moja una persona que corre bajo la lluvia es una situación muy caótica y difícil de describir. Sin embargo, la lógica nos dice que esta aproximación lineal es bastante acorde con la realidad. Además de este análisis matemático, existen intentos de recoger pruebas empíricas. Los Cazadores de Mitos dedicaron dos programas a este asunto: en el primero, les salió que el que más corría, más se mojaba. Sin embargo, ese experimento fue realizado con aspersores. Más tarde lo repitieron con lluvia real, que es más homogénea, y obtuvieron que el que más corre se moja ligeramente menos. Este último resultado parece estar más acorde con lo obtenido en nuestro análisis.

\left . \begin{matrix} Q_x = Q_{b,x} + Q_{h,x} \\ Q_{b,1} = Q_{b,2} \\ Q_{h,1} > Q_{h,2} \end{matrix} \right \} Q_1 > Q_2

Por lo tanto, llegamos a la conclusión de que si corres bajo la lluvia, te mojas ligeramente menos.

NOTA: Otros han llegado a la misma conclusión con otros métodos. Incluso hemos encontrado una aplicación para calcular cuánto te mojarías variando varios parámetros.

38 comentarios sobre “Por qué correr bajo la lluvia SÍ merece la pena”

  1. Me ha gustado esto mucho. Pero tengo una duda. Si la distancia al refugio es la misma para la persona que anda que para la que corre, la persona que corre llegará antes al refugio y por lo tanto permanecerá menos tiempo bajo la lluvia. ¿Esto no influiría en alguna de las ecuaciones? ¿O ya lo habéis calculado y no me he dado cuenta?
    De todas maneras, yo corro bajo la lluvia dependiendo de las ganas que tenga de correr, de la cantidad de agua que llueva y de si tengo paraguas o no,… XDDD

  3. Maldición, esta tarde he visto ese capítulo (el inodoro explosivo) y había empezado a escribir algo. Esta entrada es genial, así que a borrar lo hecho.

  4. Sip, José Luis, la diferencia de tiempo está considerada. De hecho: a tiempos iguales, el que corre más, se moja más. Es cuando consideramos la distancia como fija, que merece la pena correr.
    ¡Siento haberte pisado la entrada Eugenio!

  6. Creo que habría que considerar el flujo de aire. Al correr, se desvía el flujo laminar del aire que tenemos delante, con lo que parte de las gotas de lluvia se desplazan.

  7. Me parecen buenas suposiciones de salida y los parámetros fijados son los correctos, pero a mi forma de verlo hay una gran variable que se nos escapa y va relacionada con la suposición «ladrillera»: La posición del cuerpo humano.

    Cuando alguien corre cambia mucho su posición corporal. Habitualmente se agacha la cabeza (siendo esta superficie mas frontal a la velocidad del agua) y esto provoca también que parte de la cabeza haga de «paraguas» sobre el pecho.
    En un caso más real la superficie efectiva no es igual en ambos casos. Cuando se corre (con perdón) la forma del cuerpo humano pasaría de ladrillo a una «L» invertida (mas o menos)

    Pero insisto, que me parece un gran aproximación y unos cálculos muy correctos. Bravo.

  9. @Ocularis:

    Está claro que realizamos un montón de simplificaciones. Los modelos están para eso, para linealizar los problemas reales, que son no lineales y por lo tanto no resolubles. La cuestión es si el modelo aproxima lo suficientemente bien lo que ocurre en realidad. Como dice Dexter, parece que sí.

  11. Pues yo creo que es tan fácil como la dirección del viento y por lo tanto la dirección de la lluvia en sí misma…

    Si la lluvia cae en diagonal y corres en dirección del viento parecerá que te mojas menos, porque por delante así será.

    Si la lluvia cae horizontal andando parecerá que te mojas menos porque todo va a la cabeza y hombros, pero corriendo te mojarás más por delante debido a la velocidad.

    Igual soy un tipo raro y digo cosas extrañas, así que no me hagáis mucho caso.

  12. El que va corriendo se salpica en los charcos y levanta más agua con los pies. ¿puedes añadirlo en la función? :P

  16. Haciendo algo de ingenieria aplicada, creo que es de ley decir: «Supongamos al tipo que corre bajo la lluvia de dimension puntual y masa despreciable…» xD

  18. A mi los cálculos también me parecen una muy buena aproximación y si además concuerda con la experimentación, pues me convence :-)

    Solo una cosa, Iñaki, como dices, los modelos son por definición una versión simplificada de la realidad… que la replica aproximadamente y bajo ciertas condiciones.

    Pero los modelos no tienen por qué ser lineales; muchos no lo son. Un modelo no lineal es resoluble, aunque es cierto que son «más complicados» al no cumplir el principio de superposición.

    Por ejemplo, cualquier modelo físico que incluya un cos(.) es no lineal. Un ejemplo clásico es el péndulo… y una aplicación el segway :-)

  19. Claro, y esos problemas no lineales se linealizan típicamente usando la serie de Taylor, como en el caso del péndulo.

    La mayoría de problemas no lineales, como la vibración de una cuerda, por ejemplo, se convierten en irresolubles si no imponemos ciertas restricciones. Se pueden aproximar tanto como queramos mediante métodos numéricos, pero eso ya es trabajo para ordenadores.

  20. Linealizar un modelo no lineal es una asunción más que añadir. Una asunción que podrá ser aceptable o no. Es más, a veces no es necesaria.
    Generalmente la decisión depende del uso que haces de tu modelo, por ejemplo:

    – Para estudiar el comportamiento dinámico de un sistema se suele linealizar, limitando el estudio al entorno de un punto (aunque hay herramientas para sistemas no lineales).

    – Si lo usas para simular o predecir, un modelo no lineal es perfectamente valido y será un mejor reflejo de la realidad (no lineal). Un ejemplo chulo son los modelos depredador-presa.

    – Si empleas tu modelo para optimizar un proceso —eligiendo valores óptimos para ciertos parámetros manipulables— también puedes (y probablemente debes) usar el modelo no lineal.

    Vamos, que lo que realmente quería decir es que los modelos no tienen por qué ser lineales. Linealizar es una asunción no trivial más, que puedes asumir o no, y que facilita algunas tareas. Pero no hay que olvidar que el uso de modelos no lineales es lo habitual en muchos casos.

    P.S. Reitero lo dicho, todo esto no aplica al caso de la lluvia.

  21. Te mojas menos si corres, incluso el hecho de salpicar en los charcos moja menos que hundir el pie en ellos…otra cosa es que por correr no elijas el camino adecuado y te comas más charcos
    El modelo cojonudo muchachos, me recuerda a un problema de estadística I sobre lluvia y jaulas de cerveza…o era al revés?
    Eso si, como dijo Ocularis una variable que puede ser importante al profundizar un poco es la diferencia de comportamiento del flujo de aire en ambas situaciones…

  23. Corriendo bajo la lluvia…

    Ahora que ya nos empieza a llegar el frío propio del invierno y empieza a llover más a menudo, a algunos de nosotros se nos empiezan a ocurrir cosas como si corriendo bajo la lluvia nos mojamos más o nos mojamos menos. El tema está tratado en gran …

  24. Encuentro una tontería discutir si te mojas más o menos corriendo o andando.
    No tiene ninguna utilidad práctica, es obvio que si corres llegas antes y por tanto te mojas menos.

    Sea vuestra demostración válida o no, sea la de el listo que lo sabe todo correcta o no, si tenéis que ir a algún sitio y llueve corred!

  26. otra teoría jaja… Si corres en plena lluvía, te resbalas, caes en el agua que yace en el piso, y aún más, te caen las que vienen arriba.

  28. Gracias YO, tu comentario es justamente el mismo que estaba a punto de enviar.

  29. Si generalizamos un poco mas el planteo.
    Supongamos que un Hombre 3 con dimensiones y formas exactamente iguales al hombre 1 y 2, pero este hombre se inclinara hacia adelante un angulo alfa acorde a su velocidad vm. Ese hombre no recibiria agua en la parte frontal!! y solo un poco mas en la cabeza, porque esa area es muy pequeña en relacion a la frontal.
    => se moja menos aun.
    La verdad que un hombre corriendo tiende a inclinar todo su cuerpo hacia adelante por lo tanto es de esperar que se moje un poco menos.
    Avisame a mi mail si tenes comentarios a esto que digo
    Saludos

  38. […] la lluvia cae con índice de inclinación (lo cual es lo más acorde a la realidad) podéis ver la estupenda demostración que han realizado Almudena e Iñaki en Enchufa2. Además os recomiendo está página donde se pueden introducir las variables que deseemos y […]

Comentarios cerrados.