(Gracias a José Luis)
Autor: Iñaki Úcar
Breve descanso
Los Enchufa2 nos tomamos a partir de hoy una semanita lejos de cualquier conexión a Internet que pueda tentarnos, lo que nos servirá para desentumecer un poco y a mí para ir centrándome en los exámenes de septiembre. Mentira. Sólo nos servirá para echar de menos el blog…
Y para que podáis entreteneros hasta nuestra vuelta, hemos habilitado una nueva pestaña en la sección de Archivos con cinco apartados en los que se incluyen (1) las series de anotaciones más destacadas de Enchufa2, (2) nuestras veinte anotaciones preferidas, (3) las diez anotaciones más vistas —aunque hay que tener en cuenta que este plugin está puesto hace poquito y no refleja todavía la realidad—, (4) las diez anotaciones más comentadas, y (5) diez anotaciones aleatorias que cambian cada vez que actualizáis la página. Pasad y servíos vosotros mismos.
Injusticia
Es bastante difícil no ser injusto con lo que uno ama.
(Oscar Wilde)
Heaviside, una vida dedicada a un solo libro
Algunos se refieren a él como matemático, otros como físico, y otros como físico y matemático. Sin duda, el inglés Oliver Heaviside (1850-1925) fue un genio de ambas materias, pero no encajaba en ninguna de ellas. De hecho, los físicos y matemáticos de la época lo tenían en muy poca o ninguna consideración. Si hay un rasgo fundamental que lo define, es la aplicación de poderosos métodos matemáticos para la resolución de problemas prácticos; y esta definición concuerda perfectamente con lo que hoy entendemos por «ingeniero». Muchos olvidan que Heaviside, junto con Hertz, se convirtió en el padre de la Ingeniería de Telecomunicación actual gracias a sus múltiples logros —nunca debidamente reconocidos— en el ámbito del electromagnetismo.
En los libros de texto de ciencia, como en todos los libros, se cometen errores. Lo triste del asunto es que los errores más comunes de este tipo de textos se encuentran en las notas históricas. Hay muy pocos libros que sean justos con la historia. Y, en concreto, Oliver Heaviside es uno de esos personajes peor tratados por el recuerdo. Por ello, en las presentes líneas, pretendo hacer un repaso de sus trabajos y ponerlos en el lugar que les corresponde. Como aperitivo, para abrir boca, fusilo un fragmento de un excelente artículo sobre Heaviside:
La mayoría de los alumnos de ingeniería de telecomunicaciones ignoran a uno de sus padres. H. Unz en Oliver Heaviside (185O-1925), IEEE Transactions on Education, 6: 30-33, 1963 , recomendaba que (1) se debería recordar a todos los alumnos que el cálculo vectorial es obra de Gibbs y Heaviside, (2) el vector de Poynting debería llamarse vector de Poynting-Heaviside, (3) las ecuaciones de Maxwell no relativistas para cargas en movimiento deberían llamarse ecuaciones de Maxwell-Heaviside, (4) la ecuación de la línea de transmisión o del telegrafista debería llamarse ecuación de Heaviside, (5) la transformada de Laplace debería llamarse transformada de Laplace-Heaviside, y (6) que el sistema internacional de unidades debería llamarse sistema de unidades de Heaviside.
 Heaviside fue el cuarto hijo de una familia escasa de dinero. Se convirtió en un niño huraño y retraído quizás porque su sordera (debida a la escarlatina) dificultó su relación con los otros niños. Gracias a un legado económico, pudo ser escolarizado entre 1863 y 1865, destacando como un buen estudiante. A partir de ahí se convirtió en voraz autodidacta que frecuentaba las bibliotecas. Entre 1867 y 1874 trabajó como telegrafista gracias a su tío Charles Wheatstone, coinventor de un sistema de telégrafo. Tuvo la suerte de pasar algunos de esos años en los barcos que mantenían el cable submarino tendido entre Newcastle y Dinamarca, experimentando y analizando todos los nuevos fenómenos que a menudo se presentaban. Mientras tanto, Heaviside seguía estudiando física por su cuenta. En 1870 descubrió un método para comparar fuerzas electromotrices, y en 1873 publicó una optimización del puente de Wheatstone, dándole un riguroso tratamiento matemático. Este trabajo le dio a conocer entre personalidades como Lord Kelvin y James Clerk Maxwell (dicen que incluso Lord Kelvin encontró su álgebra complicada).
Heaviside fue el cuarto hijo de una familia escasa de dinero. Se convirtió en un niño huraño y retraído quizás porque su sordera (debida a la escarlatina) dificultó su relación con los otros niños. Gracias a un legado económico, pudo ser escolarizado entre 1863 y 1865, destacando como un buen estudiante. A partir de ahí se convirtió en voraz autodidacta que frecuentaba las bibliotecas. Entre 1867 y 1874 trabajó como telegrafista gracias a su tío Charles Wheatstone, coinventor de un sistema de telégrafo. Tuvo la suerte de pasar algunos de esos años en los barcos que mantenían el cable submarino tendido entre Newcastle y Dinamarca, experimentando y analizando todos los nuevos fenómenos que a menudo se presentaban. Mientras tanto, Heaviside seguía estudiando física por su cuenta. En 1870 descubrió un método para comparar fuerzas electromotrices, y en 1873 publicó una optimización del puente de Wheatstone, dándole un riguroso tratamiento matemático. Este trabajo le dio a conocer entre personalidades como Lord Kelvin y James Clerk Maxwell (dicen que incluso Lord Kelvin encontró su álgebra complicada).
Fue precisamente en 1873 cuando cayó en sus manos el Tratado sobre electricidad y magnetismo de Maxwell. Impactó tanto al joven Oliver, que decidió dejar su trabajo y trasladarse a casa de sus padres para dedicarse únicamente a la investigación, publicando sus trabajos en las más prestigiosas revistas científicas de la época, aunque con poco reconocimiento. Heaviside rechazaba las protocolarias demostraciones de la matemática académica; se dedicaba a la matemática aplicada, y desarrollaba las herramientas formales necesarias conforme lo requería su investigación. Desarrolló un aparato matemático que, de hecho, funcionaba, pero era rechazado por sus contemporáneos por esta falta de rigurosidad en sus métodos. En una ocasión, dijo al respecto: «¿Debo entender la digestión para poder disfrutar de una buena cena?». Cuando Heaviside leyó la obra de Maxwell, inmediatamente se percató de sus importantes implicaciones, pero carecía todavía del conocimiento necesario para entender los desarrollos formales. Por ello, pasó los siguientes años estudiándola a fondo hasta conseguir entenderla hasta sus últimas consecuencias.
Entre 1874 y 1889, reformuló la teoría del telégrafo eléctrico de Lord Kelvin teniendo en cuenta dos nuevos factores: las pérdidas de la línea y la autoinducción. Y finalmente derivó la «ecuación del telegrafista», tan importante en este campo. Durante este periodo, además, acuñó varios términos que hoy en día los ingenieros de telecomunicaciones utilizamos constantemente: impedancia, admitancia, conductancia, permeabilidad, susceptancia, reluctancia… Entre ellos destaca la impedancia, que permitía la generalización de la Ley de Ohm para corriente alterna, y que consiste en añadir una parte imaginaria llamada reactancia a la resistencia (sí, él ya trabajaba con números complejos). De esta manera, en la impedancia se aunaban todos los efectos presentes en una línea de transmisión: resistencia, capacitancia e inductancia. En 1880 estudió el efecto pelicular e inventó y patentó el cable coaxial. En 1887, formuló la idea de que era posible eliminar la distorsión de una línea mediante la adaptación de impedancias (idea de la que se aprovecharon más tarde numerosas personas con varias patentes).
Sin embargo, quizás el legado más importante y menos recordado de Heaviside sea la propia teoría electromagnética que ha llegado hasta nuestros días. Maxwell murió en 1879 sin que su tratado fuese aceptado debido a la complejidad tanto teórica como matemática (basada en cuaterniones) que tenía para su tiempo. Sin discípulos y sin el maestro, fue Heaviside, a partir de 1882, el que se encomendó a sí mismo la tarea de reformular toda la teoría electromagnética para hacerla más accesible y darla a conocer. Para este trabajo, elaboró el análisis vectorial que tanto usamos los ingenieros de hoy, en contraposición a la teoría cuaterniónica antes mencionada, lo que le valió no pocas discusiones. Y gracias a esta herramienta, que más tarde se convirtió en el lenguaje para toda la física, logró sintetizar las originales 20 ecuaciones de 20 variables de Maxwell (que probablemente ningún físico de hoy reconocería) en las hoy famosas 4 ecuaciones (a este resultado también llegó Hertz por su cuenta, aunque él siempre concedió el mérito a Heaviside). El resultado final fue plasmado en el libro Teoría Electromagnética (1893, 1899 y 1912), que se convirtió en la única manera de entender las difíciles ideas de Maxwell.
También en el ámbito de las matemáticas, entre 1880 y 1887 desarrolló el cálculo operacional —hoy conocido como «transformada de Laplace»— para resolver ecuaciones diferenciales lineales, uno de los grandes avances matemáticos del siglo XIX. Y todavía tuvo tiempo, en 1882, de introducir el sistema internacional de unidades.
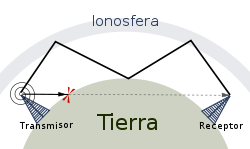
En 1902, tras la transmisión de radio que realizó Marconi el año anterior a través del Atlántico, Heaviside predijo la existencia de una capa de la atmósfera (una región de la ionosfera llamada capa de Kennelly-Heaviside) reflectora de las ondas de radio, creando una enorme guía de ondas entre la superficie terrestre y dicha capa, lo que permite transmitir mediante reflexiones más allá de la línea del horizonte. Veinte años después, en 1923, se demostró su predicción.
Durante su vida, Heaviside vivió en la pobreza. Rechazaba el dinero. Dedicado por entero a la investigación, no se planteó sacar beneficio patentando sus inventos —cosa que sí hicieron otros más tarde—. Tampoco quiso, en un principio, aceptar una pensión que finalmente le concedió el Estado por sus méritos, ni mostró entusiasmo por los premios que recibió, a saber:
- 1891: Miembro de la Royal Society de Londres.
- 1899: Miembro honorario de la American Academy of Arts and Sciences.
- 1905: La Universidad alemana de Göttingen le concede el doctorado honoris causa.
- 1908: Miembro honorario de la Institution of Electrical Engineers inglesa.
- 1918: Miembro honorario del American Institute of Electrical Engineers.
- 1921: Primer galardonado con la medalla Faraday de la Institution of Electrical Engineers.
Música y matemáticas. Física de la consonancia (2)
A petición de Zarlino en el post anterior, he creado con MATLAB unas muestras de sonido para ilustrar cómo suenan los intervalos que os indicaba el otro día en gráficas de sumas de cosenos. Recordemos que habíamos llegado a dos conclusiones:
- La disonancia está asociada a la presencia de una envolvente en la suma de los sonidos implicados en el intervalo, y esto se traduce en una sensación auditiva de «batidos».
- Estos «batidos» son más fuertes cuanto más próximos en frecuencia están los sonidos, en consecuencia, la sensación de disonancia será mayor cuanto menor sea el intervalo.
He aquí los ejemplos de audio:
Primero quiero pedir disculpas por la última muestra, porque la mezcla de armónicos que he hecho ha quedado un poco dura (aunque en esto tiene mucho que ver el ataque, algún día os contaré…). Y segundo, comentar que estoy hablando todo el tiempo de consonancia perceptiva (término acuñado por Deutsch, 1982)[1], directamente relacionada con la proximidad de frecuencias y presencia de estos batidos (Helmholtz, 1863)[2], y base de la consonancia musical. La primera constituye un concepto puramente físico y fisiológico, mientras que en la segunda influyen aspectos culturales e históricos.
Ahora hablaremos de vuestra sorpresa, la sorpresa que supongo os habrá producido escuchar la quinta muestra, porque probablemente a la mayoría de vosotros os habrá resultado más desagradable, más disonante, la cuarta muestra que la quinta. ¿No decíamos que a mayor proximidad, mayor disonancia? Eso es cierto, pero hasta ahí ha llegado únicamente nuestra teoría física sobre la consonancia: todavía no hemos tenido en cuenta nuestra fisiología, nuestro oído.
Y es que nuestro sistema auditivo es un sistema real, por tanto no ideal, con ciertas limitaciones. Podemos modelar nuestro oído como un banco de filtros que proporcionan cierta respuesta en frecuencia. En concreto, la culpable de esta respuesta es la membrana basilar, situada en la cóclea. Se trata de una membrana que se encarga de separar las frecuencias que componen el sonido para que cada una de estas frecuencias sea detectada por un grupo de células destinadas a tal efecto. Para separarlas, la membrana basilar varía en masa y rigidez a lo largo de su longitud, es decir, varía su frecuencia de resonancia y de esta manera en cada trocito vibra una sola frecuencia y las demás son atenuadas. Esto limita la resolución frecuencial del oído humano. Es decir, si hay dos tonos demasiado próximos en frecuencia, nuestro cerebro no los distingue bien y por lo tanto la sensación de disonancia es menor.
Aquí entra el concepto de banda crítica[3], que técnicamente se define como el ancho de banda de ruido alrededor de una frecuencia que es efectivo en el enmascaramiento de la misma. Coloquialmente, diremos que, dada una frecuencia, existe una porción de frecuencias alrededor de la misma en la que nos es complicado distinguir dos tonos porque están demasiado próximos, es decir, la porción de frecuencias que activan la misma zona de la membrana. Lógicamente, un oído entrenado es más capaz de discriminar tonos y por lo tanto a los músicos la quinta muestra de sonido nos suena a rayos, mientras que a otros les parecerá que suena un solo tono.
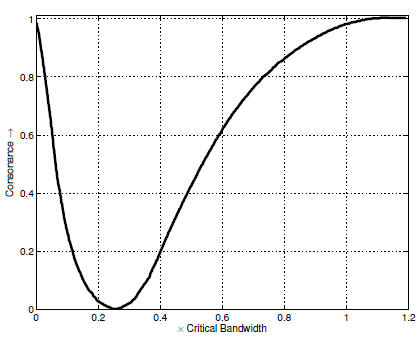
La siguiente gráfica ilustra muy bien la consonancia perceptiva en función de la porción del ancho de banda crítico que abarca el intervalo. Vemos que nuestras predicciones iniciales se cumplen a partir de 0.3, pero que también aparecen estos efectos no ideales en el origen, donde la consonancia vuelve a aumentar conforme la diferencia frecuencial tiende a cero.
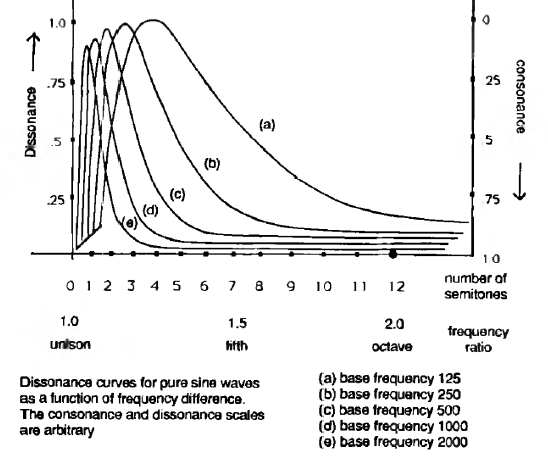
Así pues, las limitaciones de nuestro sistema auditivo hacen que, para una persona con un oído medio, la máxima disonancia perceptiva se sitúe en torno al semitono. Esto varía, puesto que el ancho de banda crítico también varía con la frecuencia. La siguiente gráfica ilustra la posición de la máxima disonancia a distintas frecuencias base:
[1] The Psychology of Music, D. Deutsch, 1982.
[2] On the Sensations of Tone as a Physiological Basis for the Theory of Music, H. Helmholtz, 1863.
[3] Tonal Consonance and Critical Bandwidth, R. Plomp y J. R. Levelt, 1965.