Autor: Almudena M. Castro

Hoy hablaremos de los principales intervalos consonantes; según los definimos el otro día: los intervalos entre sonidos cuyas frecuencias están en proporción de un número entero menor que 7. Son, por tanto, los intervalos que se obtienen al dividir una cuerda entre estos mismos números. Si tenéis una guitarra en casa, os invito a experimentar con ella.

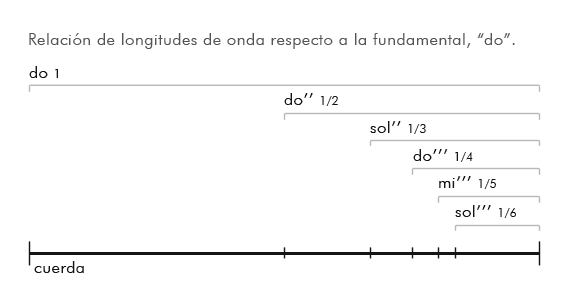
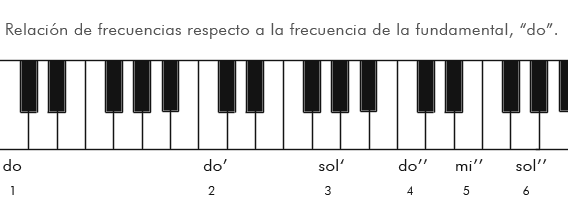
La 8ª Justa

Supongo que todos recordáis la famosa canción de sonrisas y lágrimas («do, es trato de varón»). Y, supongo que todos recordáis que, después del si «otra vez ya viene el do, do, do…». Esto, que parece trivial, denota una característica muy peculiar de nuestra audición y es que percibimos el sonido de forma cíclica o incluso circular. Este círculo se cierra cada vez que un sonido dobla su frecuencia. Es decir, si una nota determinada, pongamos, un do, tiene una frecuencia de 525 Hz, al oír un sonido con el doble de frecuencia, 1050 Hz, volvemos a reconocer «el mismo» sonido, un do, solo que esta vez, más agudo. En música este intervalo se conoce como intervalo de 8ª u 8ª Justa.

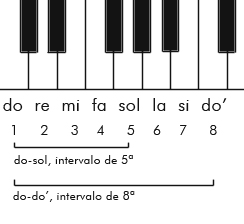
Ya mencionamos que un intervalo es la distancia que separa dos sonidos o la proporción que existe entre sus frecuencias. En música, el intervalo entre dos notas se denomina según el número de notas de la escala tradicional (do re mi fa sol la si) que las separa, incluidas las dos de los extremos. Así, el intervalo do-sol por ejemplo, sería una 5ª: 1 do, 2 re, 3 mi, 4 fa, 5 sol. El intervalo de un do al siguiente do más agudo, una 8ª: 1 do, 2 re, 3 mi, 4 fa, 5 sol, 6 la, 7 si, 8 do.

La semejanza entre dos sonidos separados por una 8ª, (esto es, dos sonidos cuyas frecuencias guardan una proporción de 2 a 1), es tal, que muchas veces no nos percatamos de que son sonidos diferentes. Por ejemplo: si se le pide a un hombre y a una mujer que canten la misma melodía, automáticamente, la mujer la cantará una 8ª más aguda que el hombre. La cantará constantemente al doble de frecuencia, pero, probablemente, no se dé ni cuenta.

Por este motivo, el otro día comentaba que los intervalos de sonidos «consonantes» son, tanto aquellos cuya proporción de frecuencias es un número entero menor que 7, como esos mismos números dividos o multiplicados por potencias de dos, ya que, cada vez que duplicamos la frecuencia de un sonido, volvemos a obtener, prácticamente, el mismo sonido. Supongamos que un do tiene frecuencia 1 y, un sol, tiene frecuencia 3 (omito las unidades pues son datos inventados y lo único que nos interesa es la proporción, no los Herzios reales). Las frecuencias 3/2, 3/4, 6 ó 12 también corresponderán a distintos soles de la escala, sumamente parecidos al sol de frecuencia 3. Tan parecidos que el intervalo do-sol resulta siempre consonante, sea cual sea el sol que tomemos.

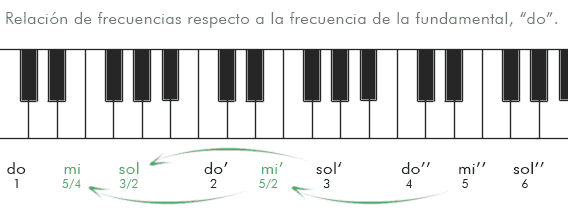
La 5ª Justa

Precisamente el siguiente intervalo consonante es el de 5ª Justa. Al duplicar la frecuencia de una nota cualquiera por dos, obtenemos la misma nota más aguda. Al triplicarla, obtenemos su 5ª (aunque en una escala más aguda). Es un intervalo fundamental, pues los griegos lo tomaron como base de su sistema musical y aún hoy sigue revelándose en la base de la armonía tonal.

La 3ª Mayor

La 3ª Mayor se obtiene al multiplicar por 5 la frecuencia fundamental. Este intervalo tardó bastante más en ser aceptado, en parte porque los griegos no le prestaron la menor atención. Sin embargo, los que sepáis algo de música, sabréis reconocer en esta interválica (fundamental, 3ª y 5ª), el acorde de triada básico en armonía tonal.

El otro día mencionamos que varios sonidos, sonando a la vez, podían resultar agradables (consonantes) o desagradables (disonantes). Ambos conceptos (disonancia y consonancia) han tenido distintos significados a lo largo de la historia, pero, por simplificar, diremos que dependen del «intervalo» que los separa. Un intervalo es la «distancia» entre dos sonidos (por ejemplo: la distancia de do a re, es menor que la distancia de do a fa). Auditivamente percibimos esta distancia como algo lineal (la distancia de do a re es de un tono o una 2ª Mayor). Físicamente se corresponde con la proporción entre las frecuencias de los dos sonidos. Y aquí viene lo mejor: cuando dicha proporción responde a un número «sencillo» (1, 2, 3, 4, 5, 6), los sonidos son consonantes, si la proporción responde a un número «raro» (1.35, 3.79), es probable que resulten disonantes. Evidentemente se trata de una cuestión bastante más compleja, con su razón de ser que iré explicando poco a poco, pero en principio se puede afirmar que: dos sonidos son consonantes si la proporción entre sus frecuencias es un número entero menor que 7 ó múltiplos y submúltiplos de potencias de 2 del mismo, (3 ó 3/2, 3/4, 3/8, 6, 12, 24 etcétera).

Esto, a los griegos, con el vicio que tenían con las proporciones, les fascinaba. Evidentemente, en el siglo VI a.C., Pitágoras no sacaba el afinador para conocer la frecuencia en Herzios de un sonido, pero él fue el primero en descubrir la relación entre lo grave o lo agudo que resultaba y las características del cuerpo que lo producía (tamaño, masa, tensión).  Cuenta la leyenda que el filósofo hizo su hallazgo al pasar por una herrería: los yunques de distintos tamaños producían sonidos diferentes. Sin embargo, para la normalización de los «intervalos» musicales y las escalas que aún hoy en día utilizamos, utilizó un instrumento de cuerda.

Pitágoras observó que cuando divía una cuerda en proporciones exactas, los sonidos resultantes eran armónicos, mientras que si se desviaba de esta proporción, los sonidos resultaban disonantes. Esto se corresponde con lo que comentábamos antes: una cuerda dividida por la mitad produce un sonido cuya longitud de onda es mitad de la del sonido de la cuerda entera (su frecuencia, por tanto es doble), una cuerda dividida por tres produce un sonido cuya frecuencia es triple, etcétera.

Para los griegos, la música era la base de su filosofía pues en ella podían comprobar empíricamente que lo proporcional era bello (armónico, consontante) y lo bello era bueno. Probablemente, si el Partenón hubiese sido un poquito más alto, o sus columnas un poquito más anchas, la desproporción hubiese sido difícil de percibir. Sin embargo, en música, los intervalos debían ser exactos para ser consonantes. Solo mediante el sonido, las matemáticas (la verdad última de todas las cosas) y su belleza resultaban claramente perceptibles.

Por todo ello, la música se consideraba, un estudio fundamental y un medio para la purificación del alma (como la medicina lo era para el cuerpo). O, en palabras de Platón:

La música es para el alma lo que la gimnasia para el cuerpo.

A raíz de un post del Otto Neurath, surgieron dudas acerca de los conceptos contrapunto y armonía. Son nociones utilizadas a menudo en música y, sin embargo, resultan difíciles de explicar. Armonía, en concreto, es un concepto bastante abstracto que hace referencia al orden y la estructura interna del lenguaje musical, equivalente quizás a la sintaxis del lenguaje hablado. Así, los distintos sonidos musicales siguen cierta jerarquía dentro de una pieza, se agrupan en acordes, se acompañan, sustituyen o adornan de distintas maneras, tienen mayor o menor importancia, se combinan de un modo u otro…

Este «orden», en la música occidental, no responde a una cuestión puramente cultural o convencional. Cuando en música hablamos de tónicas, dominantes, consonancias o disonancias, hacemos referencia a una tradición que ha ayudado a consolidar estos conceptos musicales y sus distintos «roles», pero también a las cualidades intrínsecas del sonido y nuestra forma de percibirlo. Por ello resulta ser cierto aquello de que la música y las matemáticas están íntimamente relacionadas: pero no, como podría llegar a pensarse, porque los músicos se inspirasen en proporciones áureas y otras cábalas parecidas, sino porque las características del lenguaje musical occidental obedecen en gran parte a cuestiones puramente acústicas, y estas, en último término, son explicables mediante matemáticas.

Esta cuestión es bastante compleja y requeriré más de una entrada y más de dos para desarrollarla adecuadamente. Como una primera aproximación basta saber que la característica fundamental de la música occidental es la polifonía. Ninguna otra tradición ha cultivado hasta tal punto la combinación simultánea de distintos sonidos. Esto llevó a descubrir que determinados sonidos, sonando a la vez, resultaban agradables, consonantes o armónicos y otros, sin embargo, resultan sumamente desagradables, disonantes o inarmónicos. Este sencillo fenómeno es el origen de las escalas musicales que manejamos aún actualmente, el sistema tonal y los acordes. Todo ello es explicable, en último término, por el desarrollo lógico de la polifonía.