Autor: Almudena M. Castro

Dios está en todo

Almudena M. Castro4 comentarios

Esta tía no sé si será clériga, de lo que no cabe duda es que es una gran humorista.

El ayuno y Jesús nos han abierto muchas puertas como, por ejemplo, ahora; la puerta maravillosa de Madrid. El otro día yo pensaba en la crisis y en dónde estaría todo el dinero del mundo, y Dios ha puesto ese dinero en la mano del Real Madrid para contratar a Kaká y para nosotros fue una bendición.

La esposa de Kaká, Caroline Celico, a quien corresponden estas palabras, es predicadora evangelista. Sin duda se habrá inspirado en el famoso pasaje del Evangelio de Mateo, en el que Jesús proclama:

Es más fácil que un camello entre por el ojo de una aguja, que el que un rico entre en el Reino de los Cielos.

Feliz 40 aniversario

Almudena M. Castro3 comentarios

viajeLuna

Hace 40 años el hombre pisó por primera vez la Luna, pero el viaje llevaba muchos años fraguándose en su imaginación. Quizás ello explica, en parte, el empeño que pusieron los países en la carrera espacial o la fascinación que sintieron los millones de espectadores que asistieron, a través de sus pantallas, a la hazaña del Apolo 11.

Una de las primeras películas de la historia del cine ya escenifica este viaje espacial, (por aquel entonces, solo imaginario): se trata de Viaje a la Luna, pionera del género de la ciencia ficción y rodada por George Mélies en 1902. Esta fecha es un dato bastante impresionante, teniendo en cuenta que el invento de los hermanos Lumiére data de 1894.

La película está basada a su vez en dos obras literarias anteriores:  The First Men in the Moon de Herbert George Wells y una novela de Julio Verne que a muchos os sonará; De la Tierra a la Luna. En ella se intentan describir, por primera vez, los problemas científicos que entrañaría enviar un objeto a la Luna, todo ello en una fecha tan temprana como 1865.

Cabe pensar, entonces, que quizás Einstein tenía razón al afirmar que la imaginación es más importante que  el conocimiento, y es que a veces constituye la motivación y el imprescindible primer paso hacia cualquier logro.

Entradas relacionadas:

Canción a la Luna de la ópera Rusalka, Op.114 de Dvořák

Almudena M. Castro1 comentario

Ver vídeo

Aprovechando que mañana se cumple el 40 aniversario de la llegada del hombre a la Luna, os presento esta bellísima aria de Antonín Dvořák, perteneciente a su ópera Rusalka.

Dvořák fue uno de los músicos más representativos del nacionalismo checo, junto con Smetana, de quien hablamos en su día, y Janáček. Probablemente Dvořák sea el más conocido. De hecho, casi todos habréis escuchado alguna vez fragmentos de la célebre Sinfonía del Nuevo Mundo, o las Danzas eslavas, por ejemplo.

Su ópera Rusalka, la novena que escribió, no es menos conocida. Fue estrenada en Praga en 1901 y tuvo un gran éxito entre el público checo (no tanto entre el europeo). Está dividida en tres actos y cuenta una historia que, sin duda, os resultará familiar. La rulsalka, según la tradición eslava era una especie de sirena-fantasma que vivía en el fondo de los ríos. En el libreto de esta ópera, escrito por Jaroslav Kvapil, Rusalka es una ninfa acuática enamorada de un príncipe, que desea hacerse humana para poder estar con él. Para ello acude Jezibaba, la bruja del lago. La bruja atiende la petición de Rusalka, pero a cambio, le arrebata su voz y le advierte de que, si no logra el amor del príncipe, dejará de ser ninfa o humana y estará condenada a vagar en soledad por el lago llevando la muerte a los hombres. Rusalka accede y toma una poción que la convierte en humana.

Cuando el príncipe la encuetra, la lleva a su palacio con la intención de casarse con ella. Sin embargo su mudez lo contraría. Cuando una princesa extranjera llega al palacio, el príncipe se enamora de su hermosa voz y olvida rápidamente a Rusalka. Pronto le declara su amor a la princesa, pero ésta lo rechaza y le dice que siga a Rusalka al infierno.

En este punto la versión de Dvořák se vuelve bastante más macabra que la de Disney (como toda  ópera que se precie, ésta no podía tener un final feliz). Rusalka es condenada y, desesperada, le pide ayuda a la bruja Jezibaba. Ésta le indica que debe matar al príncipe, pero ella se niega. A todo esto, el príncipe recuerda su amor por Rusalka y, desolado, la busca sin descanso. Cuando al fin la encuentra, le pide perdón y le ruega que lo bese. Rusalka le advierte que si lo hace, morirá, pero a él no le importa. Por fin se besan y el príncipe muere dichoso.

La Canción a la Luna es un aria perteneciente al primer acto de la ópera. En ella, Rusalka le habla a la Luna de su amor por el príncipe y le pregunta si él la corresponde. Podéis pinchar en el link para leer la letra traducida al castellano. En el vídeo, la soprano Renée Fleming interpreta magistralmente esta aria. A los menos aficionados al canto lírico les recomiendo la versión instrumental a cargo del violinista Joshua Bell.

Música y matemáticas. La afinación pitagórica. El origen de la escala heptatónica

Almudena M. Castro17 comentarios

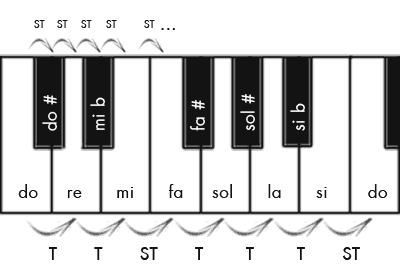
¿Alguna vez os habéis preguntado por qué son así las teclas de un piano? El teclado sigue un patrón de 7 teclas blancas entre las que se intercalan 5 negras: un total de 12 teclas por octava. Las teclas blancas corresponden a las notas de la escala natural (do, re, mi, fa, sol, la, si), las teclas negras son las notas alteradas (do#, mib, fa#, sol#, sib). Entre cada tecla y la siguiente, sea blanca o negra, hay siempre el mismo intervalo: un semitono (ST), la mitad de un tono (T).  Pero entonces, ¿por qué no están todas las teclas al mismo nivel?, ¿por qué algunas notas se consideran «naturales» y otras «alteradas»?, ¿por qué los tonos y semitonos se distribuyen de esa manera y no otra en la escala natural (T, T, ST, T, T, T, ST)?, ¿por qué tiene precisamente 7 notas? (la escala pentatónica, característica de oriente, por ejemplo, sólo tiene 5). La respuesta, de nuevo, está relacionada con Pitágoras.

teclado

La afinación por 5as

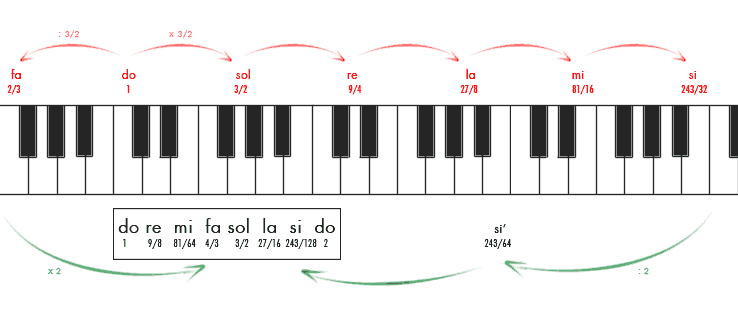
El lunes os conté como la 5ª de cualquier sonido se obtiene al multiplicar su frecuencia por 3. Sin embargo, así obtenemos su quinta una octava más aguda. En rigor, tendríamos un intervalo de 12ª (una 8ª más una 5ª: como al medir los intervalos tomamos las dos notas de los extremos, las sumas en música no funcionan, siempre dan uno de más). Ese mismo sonido, una octava baja, se hallaría en una proporción de 3/2 respecto a la fundamental, y ésta es la proporción que Pitágoras tomó como base de su sistema musical.

Para reconstruir este sistema, partiremos de la nota do y supondremos, nuevamente, que su frecuencia es 1. A partir de ahí, la multiplicaremos sucesivamente por 3/2 para obtener cada nuevo sonido de la escala natural. La mayoría de estos sonidos aparecerán en escalas más agudas, pero para obtener estos sonidos en la escala original no tenemos más que bajarles una o varias veces de 8ª, esto es: dividir su frecuencia entre dos. El resultado es el que podéis ver en la siguiente imagen:

teclado-quintasCon estos datos podemos observar varias particularidades de la escala:

intervalosgráficamejorado

  1. Existen cinco intervalos de mayor tamaño y dos claramente más pequeños. Los intervalos más pequeños se encuentran entre el mi y el fa, y entre el si y el do agudo. Si observamos el teclado del comienzo, vemos que entre las teclas blancas correspodientes a estas notas no hay ninguna tecla negra: son los dos únicos intervalos de semitono que encontramos en la escala natural.
  2. La diferencia de frecuencias va aumentando según nos acercamos al agudo. No obstante, nosotros percibimos los intervalos de tono como iguales debido a que nuestra percepción es logarítmica (para intervalos iguales, donde a y b son frecuencias, se cumple que loga – logb = cte).
  3. Podríamos seguir añadiendo quintas obteniendo así sonidos intermedios, pero los intervalos comenzarían a ser menos homogéneos. No obstante, este es el origen de la escala cromática, como veremos el próximo día.

También podemos observar que esta escala tiene ciertos defectos o incoherencias.

  1. El semitono no es la mitad exacta de un tono, (256/243 ≠ √9/8). Por ello, mediante esta afinación, obtendremos dos tipos de semitonos distintos: cromáticos y diatónicos, como veremos el próximo día.
  2. La tercera dista mucho de ser «consonante», según la definición que dimos en un principio y la proporción que determinamos el pasado lunes (81/64 = 1,265625 ≠ 5/4 = 1,25). La tercera en esta escala resulta un poco disonante al ser mayor de lo que debería, y se la suele llamar ditono pitagórico.

Los modos griegos

Los griegos no utilizaban preferentemente la escala de do. En estas entradas la tomamos como referencia por ser la escala que se utilizó sistemáticamente en la música occidental a partir del Renacimiento (aproximadamente). Hoy la conocemos como escala diatónica Mayor. A veces se utiliza también la escala diatónica menor, que sería la escala de los sonidos naturales (las teclas blancas) solo que empezando desde la (T, ST, T, T, ST, T, T).

Los griegos, en cambio, tenían 8 escalas diferentes llamadas modos. El patrón interválico seguía siendo el mismo que el que acabamos de describir, solo que empezando desde distintos puntos de la escala. El modo más importante para los griegos, por ejemplo, era el modo dórico; la escala que va de mi a mi (ST, T, T, T, ST, T, T).

Entradas relacionadas:

Inmortales (2)

Almudena M. Castro

El disco ha de estar rayado en ese sitio, porque hace un ruido raro. Y hay algo que aprieta el corazón: esa tosecita de la aguja en el disco no afecta en absoluto a la melodía. Está tan lejos, tan lejos, atrás. También lo comprendo: el disco se raya y se gasta, quizá la cantante haya muerto; me iré, voy a tomar el tren. Pero detrás de lo existente que cae de un presente a otro sin pasado, sin porvenir, detrás de esos sonidos que día a día se descomponen, se descascaran y se deslizan hacia la muerte, la melodía sigue siendo la misma, joven y firme, como un testigo despiadado.

(Jean-Paul Sartre, escritor, filósofo y dramaturgo francés, en La Náusea)