Ya están en marcha los grupos de debate del V Congreso de Comunicación Social de la Ciencia que se celebrará del 10 al 12 de marzo en Pamplona. En la página del mismo, unaNUEVACULTURA.es, podéis encontrar toda la información y os invitamos a participar en los citados grupos de debate:
Categoría: Ciencia
Artículos de divulgación científica.
Congelando el tiempo
Gracias a New Scientist, descubro la fotografía de Harold Edgerton un artista ingeniero estadounidense del siglo XX, que trabajó sobre la representación gráfica del movimiento.
Precisamente, la invención de la fotografía supuso un gran avance en este campo, pues permitía congelar instantes hasta entonces «invisibles» (por lo fugaces). Gracias a ello, Eadweard Muybridge quiso capturar el galope de un caballo en varias fotografías sucesivas, convirtiéndose así en un precursor del cine.
El sistema usado en muchas de las fotografáis de Edgerton, sin embargo, se basaba en plasmar distintos estadios de un mismo movimiento en una sola fotografía. Para ello utilizaba tiempos de exposición prolongados (tanto como el movimiento que quería retratar) y un estroboscopio que iluminaba la escena de forma intermitente, evitando así que la imagen se convirtiese en un barrido indescifrable.
El estroboscopio había sido ideado por el matemático austríaco Simon von Stampfer hacia 1829 y permitía emitir flashes sucesivos a una frecuencia regulable. Sin embargo, Edgerton amplió sus posibilidades y lo llevó al campo de la fotografía. En 1926, con apenas 23 años y siendo aún estudiante en el Instituto Tecnológico de Massachusetts, desarrolló un tubo de flash capaz de producir destellos de elevada intensidad en tan sólo 1/1,000,000 de segundos. También desarrolló diversos sistemas para lograr tiempos de exposición ínfimos. Su cámara de alta velocidad sincronizaba el obturador con cada flash del estroboscopio, logrando así rodar secuencias a cámara extremadamente lenta. En la década de los 40, ideó asímismo la cámara rapatrónica para fotografiar explosiones nucleares con todas las dificultades que ello implicaba (una luz cegadora captada a kilómetros de distancia), y tiempos de exposición de apenas 10 nanosegundos (1/100,000,000 segundos). Estos sistemas le permitieron capturar instantes aislados de una duración ínfima, fotografías fugaces que muchos habréis visto:
El valor estético de estas imágenes es indudable. De hecho, Edgerton recibió varios premios de fotografía en vida, colaboró con artistas reconocidos como Gjon Mili y su obra se llegó a exponer en multitud de museos, incluido el prestigioso MOMA de Nueva York. Incluso colaboró en un corto documental ganador de un Óscar: Quicker’n a Wink. De nuevo, un logro científico había abierto puertas a la creación plástica. Sin embargo, Edgerton negaba ser un artista en absoluto:
No me tomen por un artista. Soy ingeniero. Persigo los hechos. Sólo los hechos.
Yo tengo mis dudas. Y a vosotros qué os parece, ¿ciencia o arte?
Aerodinámica
Me ha recordado esta fotografía una entrada de Maikelnai sobre ciertas semillas voladoras. No tengo ni idea sobre aerodinámica, pero preguntándole a San Google he encontrado este link, algunas citas y, sobre todo, montones de imágenes que dan bastante idea sobre la forma de este búho.
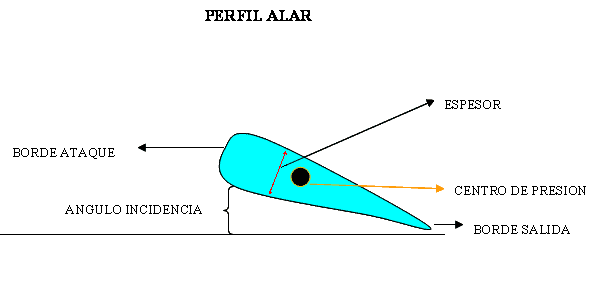
Supongamos que necesitamos diseñar una superficie que posea una baja resistencia; la forma ideal sería aquella cuyo perfil sea más romo o grueso en la parte de proa y más puntiaguda en la zona de popa.
La llamada forma de gota, es la forma aerodinámica ideal para velocidades subsónicas.
Actualización por Iñaki (05/08/2013)
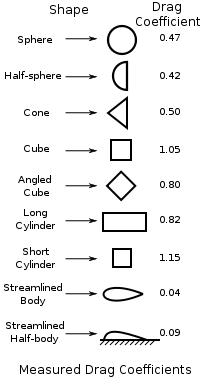
Como bien apunta @carloscasanueva (¡gracias por el aporte!), esta forma de gota en inglés se denomina streamlined body, que no tiene una traducción directa, pero podríamos entenderlo como cuerpo esculpido por líneas de corriente. Además, en la Wikipedia en inglés encontramos una reveladora imagen que muestra distintas formas y sus correspondientes coeficientes de arrastre (a menor coeficiente, más aerodinámica). Como se aprecia, la forma de gota de agua posee el coeficiente más bajo, lo que la hace muy buena para velocidades subsónicas.
Desbarrada en los Goya
Ayer tuvo lugar la gala de los Premios Goya, ese acto que organiza la Academia todos los años para mirarse un ombligo lleno de pelusas que nunca se han molestado en quitar. Sólo vi un trocito. La única motivación que tenía para ello era que estaba puesto en la tele mientras yo cenaba y que salía Buenafuente, pero su guión era pésimo y él parecía poco convencido de lo que estaba haciendo, así que me apresuré en la cena y volví al ordenador. Sin embargo, en ese rato vi suficiente: entre premios e intervenciones de Andreu, se intercalaban citas célebres, y una de ellas fue la siguiente, de Luis Buñuel:
La ciencia no me interesa. Ignora el sueño, el azar, la risa, el sentimiento y la contradicción, cosas que me son preciosas.
Con dos cojones. Veo en Twitter que no he sido el único en atragantarme con la sopa. Con la Ministra de inCultura allí presente, casi es como si hablara el mismo Gobierno. Lo sueltan ahí, con letras bien grandes y voz en off, y la masa se regocija y aplaude. Si os digo la verdad, he sentido vergüenza ajena. Creo que habrían hecho bien en medir sus palabras, porque esto supone un revés intolerable en una televisión que no se prodiga precisamente en temas científicos.
Y es que estamos con lo de siempre: si lo tuyo es la ciencia, tienes que saber de todo; si lo tuyo son las artes o las letras, no tienes por qué saber hacer la o con un canuto en materia de ciencia. Lo discutíamos el otro día en clase en un tema similar, con el profesor de Organización y Dirección de Empresas, a raíz de un artículo que recogía la opinión de varios consejeros delegados sobre sus respectivos directores del departamento técnico. Al parecer todos se quejan de que estos no tienen una visión global de todas las tareas que cubre la empresa y que, puesto que cubren el resto de departamentos, deberían aprovechar para aprender lo que allí se hace. A lo que yo digo: y el resto de departamentos, ¿no debería aprender lo que se hace en el departamento técnico, ya que está cubierto por él?
Total, que al cine español no le interesa la ciencia. Tampoco le interesa el público, y lo demuestran con cada nueva película.
Problema de nitidez: la solución
A continuación, la solución al problema propuesto ayer. De ahora en adelante, asumiremos que la bicicleta se desplaza por el eje real de izquierda a derecha (de los números negativos a los positivos o, dicho de otra manera, con velocidad positiva) y que captamos la instantánea justo a su paso por el origen. De esta forma, podemos usar el sistema de coordenadas polares con comodidad.
El problema reside en aplicar el principio de superposición de movimientos: por un lado tenemos el movimiento rectilíneo horizontal de la bicicleta, de izquierda a derecha, como hemos comentado; por otro lado, tenemos el giro de la rueda. Esto se denomina movimiento rototraslatorio.
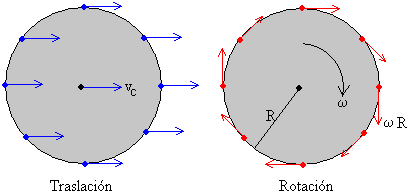
Obviamente, habrá puntos —como se puede intuir a partir de la imagen— en los que la velocidad de rotación se cancelará con la velocidad de traslación y, por ende, saldrán en nuestra fotografía. Para resolverlo, habrá que descomponer la velocidad de rotación de todos los puntos de la rueda en sus componentes vertical y horizontal. Tras esto, a la componente horizontal hay que sumarle la velocidad de traslación y volver a componer el módulo del vector velocidad mediante Pitágoras.
En primer lugar, si la rueda es de radio 
Para hallar las componentes vertical y horizontal de dicha velocidad, es fácil ver que basta con multiplicar por el 
Si manipulamos esta expresión convenientemente, podemos llegar a lo siguiente:
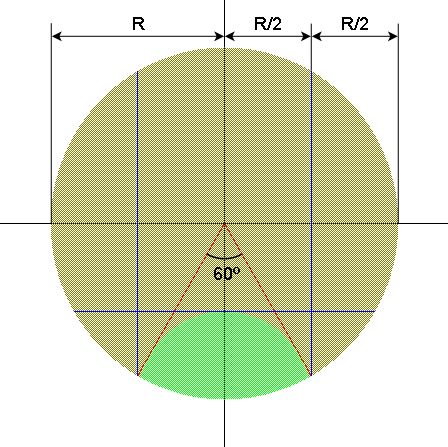
Que no es otra cosa que la expresión, en coordenadas polares, de un círculo con centro en 
