La ecuación del botijo

Iñaki Úcar17 comentarios

Corría el año 1990 cuando Gabriel Pinto, profesor de Química en la Escuela Técnica Industrial de la Universidad Politécnica de Madrid, se compró un botijo y se dispuso a tomar medidas en sus ratos libres del conocido efecto botijo. Su objetivo era construir un modelo matemático válido para cualquier tipo de botijo o recipiente cerámico poroso que relacionase sus características con su capacidad de enfriar el agua.

El dispositivo experimental constaba de un botijo clásico en el que se introdujeron 3,2 litros de agua a 39 ºC y este, a su vez, se mantuvo a esa misma temperatura en un horno de laboratorio, con una humedad relativa del 42%. Cada cierto tiempo, Pinto fue midiendo la masa del botijo (para determinar la masa de agua evaporada) así como la temperatura del agua. De esta manera, observó que en unas 7 horas el agua se había enfriado 15 ºC, alcanzando los 24 ºC. A partir de ese punto, el agua comenzaba a calentarse de nuevo, debido a que ya se había evaporado aproximadamente medio litro. Al cabo de tres días, las últimas gotas de agua que quedaban volvían a alcanzar la temperatura ambiente de 39 ºC.

A la par, Pinto desarrolló un modelo matemático, como hemos comentado, que iba ajustando gracias a los datos experimentales. Había considerado multitud de factores, sin embargo, había algo que seguía sin cuadrar: las ecuaciones le conferían al botijo una capacidad ilimitada de enfriar.

Entonces fue cuando apareció el otro protagonista de nuestra historia, José Ignacio Zubizarreta, también profesor de Química. Él fue el que dio con el detalle que faltaba en el modelo, algo que Pinto había pasado por alto: el calor de radiación que aporta el aire que se encuentra en el interior del recipiente. Con esta última consideración, los datos casaban a la perfección.

Así, en 1995, ambos profesores publicaron en la revista Chemical Engineering Education, vol. 29, de Estados Unidos, el artículo An ancient method for cooling water explained by means of mass and heat transfer.

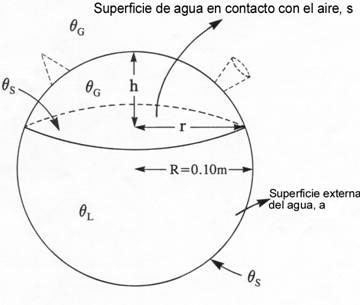
El resultado del trabajo, de carácter pedagógico, fueron dos ecuaciones diferenciales que relacionaban todos los parámetros. El modelo seguido, una vez más, empieza como el famoso chiste de la vaca: supongamos que tenemos un botijo con geometría esférica… Y, por fin, las susodichas:

-\displaystyle\frac{dV}{dt}=K^\prime\cdot a\cdot(H_s-H)

V\cdot C_p\cdot\left(\displaystyle\frac{dT}{dt}\right)=h_c\cdot a\cdot(T_g-T_s)+f\cdot\epsilon\cdot\sigma\cdot\left[(273+T_g)^4-(273+T_s)^4\right]\cdot

\cdot(4\pi r^2-s)-U\cdot a\cdot(T-T_s)-\lambda_w\cdot\left(\displaystyle\frac{dV}{dt}\right)

Donde:

  • V \equiv volumen o masa de agua
  • C_p \equiv capacidad calorífica del agua
  • T \equiv temperatura del agua
  • t \equiv tiempo
  • h_c \equiv coeficiente de convección
  • a \equiv superficie externa del agua
  • T_g \equiv temperatura del aire
  • T_s \equiv temperatura de la superficie del agua
  • f \cdot \epsilon \cdot \sigma \equiv coeficiente de radiación de calor
  • 4 \pi r^2 \equiv superficie total del botijo
  • s \equiv superficie del agua en contacto con el aire
  • U \equiv coeficiente de transmisión de calor del agua
  • \lambda_w \equiv calor de vaporización del agua
  • K^\prime \equiv coeficiente de transferencia de masa para el agua
  • H_s \equiv humedad de saturación
  • H \equiv humedad del aire

botijo

Suite para violoncello No.1, de Bach

Almudena M. Castro11 comentarios

Ver vídeo

Los exámenes empiezan y no tengo mucho tiempo para comentar esta pieza como debería. Sólo os remito a la explicación sobre contrapunto que escribí la última vez que hablamos de Bach.

Bach escribió un total de seis suites para violoncello solo, todas ellas muy recomendables. Elijo la primera quizás por ser la más reconocible y escuchada, pero cualquiera de las otras cinco merece la pena también. La forma suite se caracteriza por reunir varios movimientos, cuyo origen son distintas danzas barrocas de ritmo contrastante.  Entre estas danzas, una suite siempre debe contener: una Allemande (lenta), una Courante (francesa, rápida), una Sarabanda (española, pausada) y una Giga (inglesa, rápida y viva). Las suites de Bach añaden además un Preludio para introducir cada suite y una danza adicional entre la Sarabanda y la Giga que puede ser: un Minueto (suites 1 y 2), un Bourrée (suites 3 y4), o una Gavota (suites 5 y 6). Cada suite consta por tanto de 6 danzas diferenciadas por su estructura y sus características rítmicas.

De nuevo, música de Bach: puro ritmo, equilibrio, formas orgánicas y fluidas que se entrelazan entre sí y parecen no tener fin. En esta ocasión la interpretación corre a cargo de Rostropovich, un genio del violoncello de origen soviético (no puedo evitarlo, lo siento). En Youtube encontraréis también la excelente interpretación de Pablo Casals, que no añado a esta entrada porque la calidad de la grabación es algo peor, pero que os recomiendo encarecidamente escuchar.

Moviéndonos por el sistema solar

Iñaki Úcar1 comentario

Una de las complicaciones más grandes que tienen que salvar las sondas espaciales en su viaje por nuestro sistema solar es la de vencer la atracción gravitatoria que ejercen los diferentes planetas, satélites y el Sol, por supuesto. Se requiere una energía grandísima para escapar de estos gigantes gravitacionales. Sin embargo, este enemigo a priori puede convertirse en el mayor aliado.

En Saltando entre órbitas, Wis explica de manera sencilla qué es la órbita de transferencia de Hohmann y la asistencia gravitatoria, dos métodos sencillos, seguros y sobre todo baratos para saltar de órbita en órbita con la ayuda del tirón gravitatorio de los astros. En la Wikipedia podemos leer:

En la astronáutica y la ingeniería aeroespacial, la órbita de transferencia de Hohmann es una maniobra orbital que, bajo las hipótesis comunes de la astrodinámica, traslada a una nave espacial desde una órbita circular a otra utilizando dos impulsos de su motor. El nombre proviene del científico alemán Walter Hohmann que publicó su teoría en 1925.

orbita-tranferencia-hohmann

En astronáutica se denomina asistencia gravitacional a la maniobra destinada a utilizar la energía del campo gravitacional de un planeta o satélite para obtener una aceleración o frenado de la sonda cambiando su trayectoria.

[…] Para poder utilizar la asistencia gravitacional es necesario un correcto alineamiento de los planetas, razón por la cual las misiones espaciales tienen ventanas de lanzamiento estrictas. La misión espacial Cassini/Huygens utilizó la asistencia gravitacional de Venus en 2 ocasiones, la Tierra y Júpiter para llegar finalmente a Saturno en un periodo de tiempo de 7 años.

cassini_interplanet_traject

En el segundo método, llama la atención la existencia de la asistencia gravitatoria positiva y negativa, dependiendo de si nos acercamos a un astro por detrás o por delante, respectivamente. En ambos casos se consigue un cambio de dirección, pero, además, en el primero se consigue acelerar mientras que en el segundo deceleramos. Para explicaciones más detalladas, no dejéis de leer el artículo de Wis.

El secreto de los violines Stradivarius

Iñaki Úcar11 comentarios

La ciudad de Cremona (Italia) vio nacer, allá por el siglo XVII, los mejores violines jamás construidos, a manos del famoso luthier Antonio Stradivari. Hoy en día, sus (mal llamados) Stradivarius son valiosas piezas que alcanzan precios millonarios. Los más selectos, incluso, tienen un valor incalculable.

Desde entonces, ha habido innumerables intentos de igualar la calidad sonora de estos instrumentos con un denominador común siempre: el fracaso. Muchas son las teorías acerca del secreto que Antonio se llevó a la tumba. ¿El barniz? ¿El tiempo de secado de la madera? ¿Un tronco «especial» sacado de un río? Algunas tienen más sentido, otras son más poéticas, pero ninguna ha llevado por el momento a la reproducción de ese sonido tan característico.

La ciencia podría tener la respuesta, pero cuenta con trabas insalvables, una vez más. Al ser piezas únicas, los estudios que pueden (más bien que permiten) hacerse son limitados, de «mírame pero no me toques», que diría el refrán. Y esto, aunque ha permitido averiguar algunas cosas, es como querer estudiar un electrón con una lupa.

Sin embargo, parece que Joseph Nagyvary, profesor emérito de bioquímica de la Universidad de Texas, ha tenido más suerte. Nagyvary lleva media vida detrás del secreto de los Stradivari, y siempre ha defendido que la excepcional calidad sonora de estos instrumentos se debe a algún tratamiento químico de la madera que no ha trascendido hasta nuestro tiempo. En su último trabajo, tras enormes esfuerzos y súplicas para conseguir pequeñas muestras de madera de expertos restauradores, ha conseguido nuevos resultados que podrían destapar el ansiado secreto. Concretamente el análisis del humo de quemar las muestras ha sido el que ha aportado nuevos detalles. Nagyvary y su equipo han encontrado bórax, fluoruros, cromo y sales de hierro. Merece especial atención el heptaoxotetraborato de sodio, o bórax para los amigos, que históricamente ha sido utilizado como conservante e insecticida. Probablemente fuera utilizado por Stradivari para proteger sus instrumentos de la carcoma.

La reproducción de las cualidades de los millonarios violines Stradivarius tendría, evidentemente, serias implicaciones. Esto, sumado al misticismo que los rodea, implica un gran obstáculo para los científicos. Tal vez el famoso secreto pase por algo tan sencillo como aplicarle bórax a la madera, tal vez sea otro compuesto y este análisis de una muestra tan pequeña sea insuficiente. En cualquier caso, este es un trabajo muy importante, en mi opinión, porque pone de manifiesto la capacidad de la ciencia y abre un serio debate. ¿Merece la pena sacrificar algún instrumento para tratar de descubrir la fórmula de tan ansiado sonido?