Es bastante difícil no ser injusto con lo que uno ama.
(Oscar Wilde)
Es bastante difícil no ser injusto con lo que uno ama.
(Oscar Wilde)
A pesar de que el sistema de afinación pitagórico es el único que respecta las dos consonancias principales (8as y 5as), la incompatibilidad entre ambas daba lugar a bastantes inconvenientes, tal como vimos la semana pasada. Como alternativa se propusieron otros sistemas a lo largo de la historia, algunos basados en la consonancia de 3ª (como el sistema justo o el mesotónico), otros, en unidades interválicas más pequeñas que el semitono (sistema de Holder, por ejemplo). No tengo especial interés en estos sistemas, pues creo que no aportaron mucho al sistema actual, pero se puede hablar de ellos en otra entrada si alguien tiene interés. Finalmente, el sistema que se impuso fue el sistema temperado, o temperamento igual (en inglés Equal Temperament, ET), basado en 12 semitonos iguales y que sólo respeta la consonancia de 8ª. Todas los demás intervalos, como veremos en esta entrada, resultan ligeramente disonantes. A pesar de ello, es un sistema óptimo para la música tonal, especialmente a partir del Barroco y el Clasicismo: cada vez más llena de modulaciones (cambios de tonalidad o de «escala»), alteraciones accidentales, cromatismos (empleo consecutivo de intervalos de semitono), etcétera.
Es fácil deducir la razón de ser matemática del sistema temperado. Para ello intentaremos averiguar cuánto mide el intervalo de semitono en este sistema. Un intervalo es una proporción de frecuencias, por lo que la frecuencia de cada nota de la escala cromática, se obtendrá de multiplicar la nota anterior por la proporción (razón) correspondiente a un semitono, que por el momento llamaremos «x». Si queremos saber, por ejemplo, cuál es la frecuencia de do#, multiplicaremos la frecuencia de do por «x». Para obtener re, volveremos a multiplicar el resultado obtenido por x, (o la frecuencia de do por x2), etcétera. Por tanto, si queremos completar una 8ª con 12 intervalos iguales, necesitamos un semitono tal que al multiplicarlo 12 veces consecutivas por la frecuencia base, (pongamos 1), dé como resultado una frecuencia doble, (2, el mismo sonido una 8ª más agudo). Esto es: . Por tanto,
. Esta es la relación de frecuencias correspondiente a un semitono temperado. Este semitono es intermedio de los pitagóricos: diatónico,
, y cromático,
.
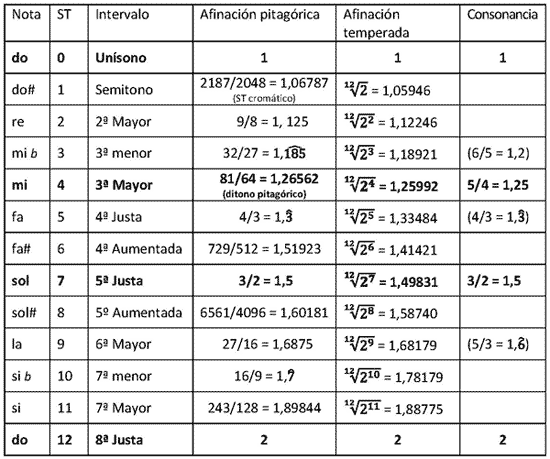
Para hallar la proporción correspondiente a cualquier otro intervalo de la escala temperada, tan sólo tendremos que elevar al número de semitonos (ST) que contiene dicho intervalo. En la tabla podéis ver una comparativa entre los intervalos pitagóricos, los temperados y los consonantes. Algunas consonancias están entre paréntesis porque son resultado de la inversión de otro intervalo consonante: la 4ªJ es una inversión de la 5ªJ (de do a sol hay una 5ªJ, de sol al do más agudo hay una 4ª), la 3ªm es el intervalo que hay entre mi y sol, ambos consonancias de do, por lo que también suele considerarse consonante, por último, la 6ªM es la inversión de la 3ªm.
También podéis apreciar las diferencias de afinación en este gráfico extraído de la wikipedia, aunque con algunos errores corregidos del original. Los puntos negros son temperados y los azules pitagóricos. El cent es una medida de afinación equivalente a la centésima parte (logarítmica, claro está) de un semitono temperado:
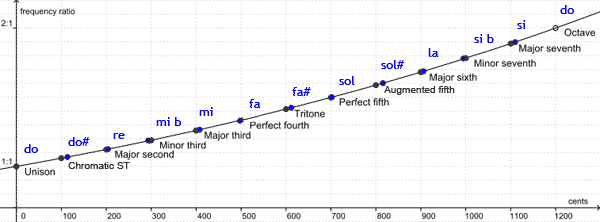
Como podéis ver, ambos sistemas son muy parecidos. Las mayores diferencias se encuentran entre las notas alteradas, especialmente al llegar al sol# (extremo del círculo de 5as). Sin embargo, si escuchamos la escala diatónica de los sonidos naturales, afinada según el sistema pitagórico o el temperado, resultan casi indistinguibles.
la 5ªJ temperada es casi idéntica a la pitagórica: difieren aproximadamente 2 cents. Para que os hagáis una idea, podéis escuchar cómo suenan dos sonidos que difieren en 1 cent, 6 ó 10 en esta página de la wikipedia. Son indistinguibles.
La diferencia entre ambas 5as recibe el nombre de schisma. Para calcular cuánto mide basta dividir la 5ª pitagórica entre la temperada, o bien, repartir la coma pitagórica entre las 12 quintas que cierran el círculo en el sistema temperado. El resultado es el mismo:
La 3ªM difiere algo más entre un sistema y otro, pero sigue siendo claramente disonante en ambos. Hasta no oírlo, yo no imaginaba cuanto, así que aquí tenéis el intervalo afinado en ambos sistemas y una 3ªM consonante para compararlos.
Para escuchar más posibles comparaciones, resulta muy útil el programa Scala del que nos habló Zarlino y cuya recomendación yo reitero.
—Mira lo que consigo que haga Pavlov: tan pronto como empiece a babear, él sonreirá y empezará a tomar notas en su pequeño cuaderno.
Algunos se refieren a él como matemático, otros como físico, y otros como físico y matemático. Sin duda, el inglés Oliver Heaviside (1850-1925) fue un genio de ambas materias, pero no encajaba en ninguna de ellas. De hecho, los físicos y matemáticos de la época lo tenían en muy poca o ninguna consideración. Si hay un rasgo fundamental que lo define, es la aplicación de poderosos métodos matemáticos para la resolución de problemas prácticos; y esta definición concuerda perfectamente con lo que hoy entendemos por «ingeniero». Muchos olvidan que Heaviside, junto con Hertz, se convirtió en el padre de la Ingeniería de Telecomunicación actual gracias a sus múltiples logros —nunca debidamente reconocidos— en el ámbito del electromagnetismo.
En los libros de texto de ciencia, como en todos los libros, se cometen errores. Lo triste del asunto es que los errores más comunes de este tipo de textos se encuentran en las notas históricas. Hay muy pocos libros que sean justos con la historia. Y, en concreto, Oliver Heaviside es uno de esos personajes peor tratados por el recuerdo. Por ello, en las presentes líneas, pretendo hacer un repaso de sus trabajos y ponerlos en el lugar que les corresponde. Como aperitivo, para abrir boca, fusilo un fragmento de un excelente artículo sobre Heaviside:
La mayoría de los alumnos de ingeniería de telecomunicaciones ignoran a uno de sus padres. H. Unz en Oliver Heaviside (185O-1925), IEEE Transactions on Education, 6: 30-33, 1963 , recomendaba que (1) se debería recordar a todos los alumnos que el cálculo vectorial es obra de Gibbs y Heaviside, (2) el vector de Poynting debería llamarse vector de Poynting-Heaviside, (3) las ecuaciones de Maxwell no relativistas para cargas en movimiento deberían llamarse ecuaciones de Maxwell-Heaviside, (4) la ecuación de la línea de transmisión o del telegrafista debería llamarse ecuación de Heaviside, (5) la transformada de Laplace debería llamarse transformada de Laplace-Heaviside, y (6) que el sistema internacional de unidades debería llamarse sistema de unidades de Heaviside.
 Heaviside fue el cuarto hijo de una familia escasa de dinero. Se convirtió en un niño huraño y retraído quizás porque su sordera (debida a la escarlatina) dificultó su relación con los otros niños. Gracias a un legado económico, pudo ser escolarizado entre 1863 y 1865, destacando como un buen estudiante. A partir de ahí se convirtió en voraz autodidacta que frecuentaba las bibliotecas. Entre 1867 y 1874 trabajó como telegrafista gracias a su tío Charles Wheatstone, coinventor de un sistema de telégrafo. Tuvo la suerte de pasar algunos de esos años en los barcos que mantenían el cable submarino tendido entre Newcastle y Dinamarca, experimentando y analizando todos los nuevos fenómenos que a menudo se presentaban. Mientras tanto, Heaviside seguía estudiando física por su cuenta. En 1870 descubrió un método para comparar fuerzas electromotrices, y en 1873 publicó una optimización del puente de Wheatstone, dándole un riguroso tratamiento matemático. Este trabajo le dio a conocer entre personalidades como Lord Kelvin y James Clerk Maxwell (dicen que incluso Lord Kelvin encontró su álgebra complicada).
Heaviside fue el cuarto hijo de una familia escasa de dinero. Se convirtió en un niño huraño y retraído quizás porque su sordera (debida a la escarlatina) dificultó su relación con los otros niños. Gracias a un legado económico, pudo ser escolarizado entre 1863 y 1865, destacando como un buen estudiante. A partir de ahí se convirtió en voraz autodidacta que frecuentaba las bibliotecas. Entre 1867 y 1874 trabajó como telegrafista gracias a su tío Charles Wheatstone, coinventor de un sistema de telégrafo. Tuvo la suerte de pasar algunos de esos años en los barcos que mantenían el cable submarino tendido entre Newcastle y Dinamarca, experimentando y analizando todos los nuevos fenómenos que a menudo se presentaban. Mientras tanto, Heaviside seguía estudiando física por su cuenta. En 1870 descubrió un método para comparar fuerzas electromotrices, y en 1873 publicó una optimización del puente de Wheatstone, dándole un riguroso tratamiento matemático. Este trabajo le dio a conocer entre personalidades como Lord Kelvin y James Clerk Maxwell (dicen que incluso Lord Kelvin encontró su álgebra complicada).
Fue precisamente en 1873 cuando cayó en sus manos el Tratado sobre electricidad y magnetismo de Maxwell. Impactó tanto al joven Oliver, que decidió dejar su trabajo y trasladarse a casa de sus padres para dedicarse únicamente a la investigación, publicando sus trabajos en las más prestigiosas revistas científicas de la época, aunque con poco reconocimiento. Heaviside rechazaba las protocolarias demostraciones de la matemática académica; se dedicaba a la matemática aplicada, y desarrollaba las herramientas formales necesarias conforme lo requería su investigación. Desarrolló un aparato matemático que, de hecho, funcionaba, pero era rechazado por sus contemporáneos por esta falta de rigurosidad en sus métodos. En una ocasión, dijo al respecto: «¿Debo entender la digestión para poder disfrutar de una buena cena?». Cuando Heaviside leyó la obra de Maxwell, inmediatamente se percató de sus importantes implicaciones, pero carecía todavía del conocimiento necesario para entender los desarrollos formales. Por ello, pasó los siguientes años estudiándola a fondo hasta conseguir entenderla hasta sus últimas consecuencias.
Entre 1874 y 1889, reformuló la teoría del telégrafo eléctrico de Lord Kelvin teniendo en cuenta dos nuevos factores: las pérdidas de la línea y la autoinducción. Y finalmente derivó la «ecuación del telegrafista», tan importante en este campo. Durante este periodo, además, acuñó varios términos que hoy en día los ingenieros de telecomunicaciones utilizamos constantemente: impedancia, admitancia, conductancia, permeabilidad, susceptancia, reluctancia… Entre ellos destaca la impedancia, que permitía la generalización de la Ley de Ohm para corriente alterna, y que consiste en añadir una parte imaginaria llamada reactancia a la resistencia (sí, él ya trabajaba con números complejos). De esta manera, en la impedancia se aunaban todos los efectos presentes en una línea de transmisión: resistencia, capacitancia e inductancia. En 1880 estudió el efecto pelicular e inventó y patentó el cable coaxial. En 1887, formuló la idea de que era posible eliminar la distorsión de una línea mediante la adaptación de impedancias (idea de la que se aprovecharon más tarde numerosas personas con varias patentes).
Sin embargo, quizás el legado más importante y menos recordado de Heaviside sea la propia teoría electromagnética que ha llegado hasta nuestros días. Maxwell murió en 1879 sin que su tratado fuese aceptado debido a la complejidad tanto teórica como matemática (basada en cuaterniones) que tenía para su tiempo. Sin discípulos y sin el maestro, fue Heaviside, a partir de 1882, el que se encomendó a sí mismo la tarea de reformular toda la teoría electromagnética para hacerla más accesible y darla a conocer. Para este trabajo, elaboró el análisis vectorial que tanto usamos los ingenieros de hoy, en contraposición a la teoría cuaterniónica antes mencionada, lo que le valió no pocas discusiones. Y gracias a esta herramienta, que más tarde se convirtió en el lenguaje para toda la física, logró sintetizar las originales 20 ecuaciones de 20 variables de Maxwell (que probablemente ningún físico de hoy reconocería) en las hoy famosas 4 ecuaciones (a este resultado también llegó Hertz por su cuenta, aunque él siempre concedió el mérito a Heaviside). El resultado final fue plasmado en el libro Teoría Electromagnética (1893, 1899 y 1912), que se convirtió en la única manera de entender las difíciles ideas de Maxwell.
También en el ámbito de las matemáticas, entre 1880 y 1887 desarrolló el cálculo operacional —hoy conocido como «transformada de Laplace»— para resolver ecuaciones diferenciales lineales, uno de los grandes avances matemáticos del siglo XIX. Y todavía tuvo tiempo, en 1882, de introducir el sistema internacional de unidades.
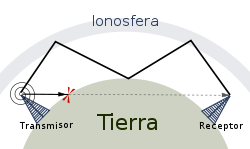
En 1902, tras la transmisión de radio que realizó Marconi el año anterior a través del Atlántico, Heaviside predijo la existencia de una capa de la atmósfera (una región de la ionosfera llamada capa de Kennelly-Heaviside) reflectora de las ondas de radio, creando una enorme guía de ondas entre la superficie terrestre y dicha capa, lo que permite transmitir mediante reflexiones más allá de la línea del horizonte. Veinte años después, en 1923, se demostró su predicción.
Durante su vida, Heaviside vivió en la pobreza. Rechazaba el dinero. Dedicado por entero a la investigación, no se planteó sacar beneficio patentando sus inventos —cosa que sí hicieron otros más tarde—. Tampoco quiso, en un principio, aceptar una pensión que finalmente le concedió el Estado por sus méritos, ni mostró entusiasmo por los premios que recibió, a saber:
Rachmaninov escribió dos conjuntos de estudios para piano o «études-tableaux» (literalmente, estudios-cuadro). Cada uno describía alguna escena o situación, si bien Rachmaninov no especificó qué pretendía retratar. El opus 39 fue publicado en 1917. Rachmaninov acababa de estar investigando sobre la obra de su contemporáneo Alexander Scriabin, recientemente fallecido en 1915, para preparar un recital en su honor. Por ello, es probable que el estilo de Scriabin influyera notablemente a Rachmaninov cuando escribió este opus y quizás también por ello, es una de mis obras preferidas.
Rachmaninov y Scriabin pueden parecer dos músicos incompatibles. Rachmaninov podría definirse bien como un músico «pop» del siglo XIX. Su música está escrita para la audiencia. Escribe a la melancolía, al dolor, de un modo idealizado y romántico (o mejor aún, postromántico: romántico al cuadrado), como todos los músicos pop. Lo cual no quita que su música tenga una gran calidad: está escrita para gustar y emocionar, como el kitsch más vulgar, sí… y lo logra hasta la médula. Su dolor es vigoroso, brillante, amplio, apasionante. A mí, personalmente, es un músico que me entusiasma.
Scriabin es todo lo contrario: el músico místico que escribe para sí mismo, el pensador que busca la filosofía y la salvación a través de su trabajo. Scriabin no es de este mundo: flota sobre él, vuela sobre él… y allí, entre las nubes, él es feliz. Extrañamente feliz. Su música parece inaccesible y en cierto modo siniestra y, a veces, cuando a Scriabin le entran dudas, muy oscura. Se puede llegar a escuchar verdadero temor en sus acordes, el miedo de alguien que se tortura por dentro, una angustia contenida que no encuentra la salida. Hay una enorme necesidad en su música… de no se sabe qué.
Creo que a Rachmaninov se le contagió parte del misterio y la volatilidad de Scriabin en este cuaderno de estudios, aunque logra conservar su dolor terrenal. Mi preferido es el número 5 en mi bemol menor, Apassionato, aunque el número 6 (Caperucita y el Lobo), o el número 3 son también muy recomendables. En el vídeo tenéis la interpretación de Kissin, siendo casi un niño.