Autor: Almudena M. Castro

Supongamos una melodía compuesta con las notas de la escala diatónica. Cada nota tendrá una altura (una frecuencia) determinada y, al unir esas alturas, obtendremos el contorno melódico que la caracteriza. Supongamos que esa melodía ha sido compuesta para una soprano, por lo que es bastante aguda. Bien, ahora, imaginemos que tenemos una contraalto, con la voz más grave que Carmen de Mairena, empeñada en cantar esta misma melodía. Tenemos dos opciones: bien dejarla dar gallos para poner a prueba nuestra resistencia a la tortura, o bien, transportar la melodía: es decir, coger su contorno (el patrón de frecuencias característico) y hacer que empiece en una nota más grave.

Esto, en teoría, debería ser bastante fácil. En la antigüedad no se andaban con remilgos y, en lugar de transportar la melodía, transportaban toda la escala sobre la que estaba construida. Así, una nota cualquiera como «do» podía tener una frecuencia de 500 Hz un día, y 635 Hz, al otro. Sin embargo, cuando aparecían en escena instrumentos de afinación fija (como un órgano o un clave), esa aleatoriedad se volvía imposible. Al estar la escala «fija», la única solución era transportar la melodía (hacer que empezase en otra nota de la misma escala) y ahí es donde aparecía el problema: en la escala heptatónica se alternan tonos y semitonos en un orden determinado. Para repetir ese patrón desde otro punto de la escala, es necesario añadir semitonos intermedios entre ciertos tonos (he aquí el origen de las notas alteradas), pero además, es necesario que todos estos semitonos sean iguales, lo que no sucede en el sistema pitagórico.

En música, existen dos tipos de notas alteradas: los bemoles (♭), que son notas «bajadas» medio tono, y los sostenidos (#), notas «subidas» medio tono. Si todos los semitonos fuesen iguales, un do# debería sonar igual que un re♭, un re# igual que un mi♭, etcétera. Estas parejas de notas a las que les corresponde el mismo sonido se denominan enarmonías. Para que sean posibles, el sonido de cada alteración debe ser intermedio de las dos notas naturales adyacentes, pero, debido a la imperfección del círculo de 5^as, en el sistema pitagórico, los bemoles se aproximan más a la nota inferior y los sostenidos, a la superior. En esta entrada veremos por qué.

La quinta del lobo

Hace dos entradas, hablamos del origen de la escala heptatónica. Bastaba con enlazar varias quintas empezando por el fa y terminando en el si. Bien, más allá del fa y del si, para medir los intervalos de 5ª, no nos bastará con contar cuántas notas separan los extremos. Si así lo hiciésemos, al contar 5 notas ascendentes desde el si, volveríamos a obtener un fa y viceversa. Sin embargo, esta quinta es más pequeña de lo normal: sólo tiene 6 semitonos, mientras que las demás tienen 7. Por ello recibe el nombre de 5ª disminuida. El sistema pitagórico se basa en la 5ªJusta de 7 semitonos (podemos observar que el sistema es coherente: con 12 quintas de 7 semitonos, igualamos 7 octavas de 12 semitonos). Así, para subir una 5ªJ desde el si, tendremos que llegar hasta el fa# y, para bajar una desde el fa, usaremos el si♭.

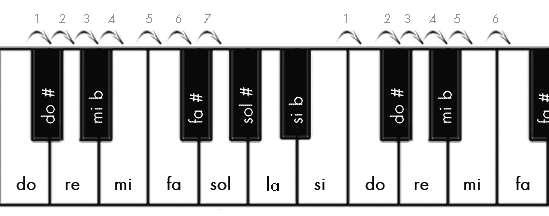
Recordemos ahora que 12 quintas bien afinadas son un poquito más de 7 octavas. Si queremos cerrar el círculo en este punto, una de las quintas tendrá que medir un poquito menos que el resto (una coma pitagórica menos), no será perfectamente consonante y sonará bastante mal. Por ello, era conocida como quinta del lobo y se procuró situarla entre dos sonidos que no se empleasen habitualmente, lo más alejados posible de la escala natural. El oscuro rincón elegido fue entre el el sol# y el mi♭ que se tomaron como los extremos del círculo de quintas. Así, para afinar los semitonos entre el la-si y el re-mi, se optó por descender dos quintas a partir del fa natural, obteniendo así si♭ y mi♭. Los sonidos fa#, sol# y do# se consiguen al subir 3 quintas desde el si.

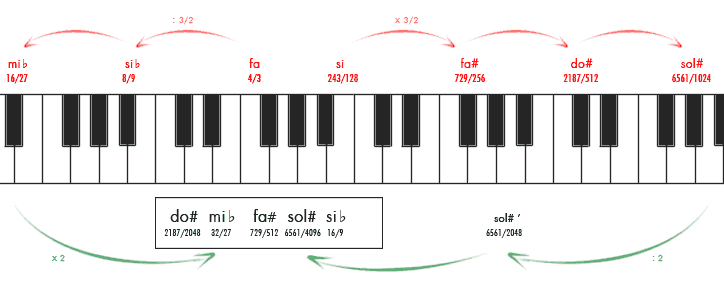
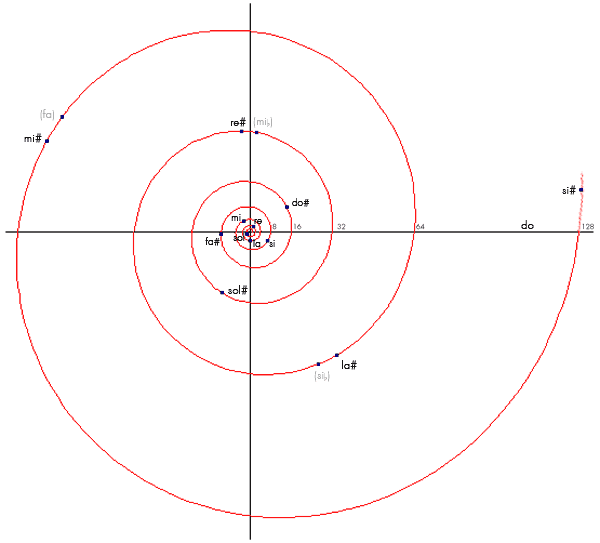
Esto significaba que, en los instrumentos de afinación fija que utilizaban este sistema, el la♭, (, afinado como un sol#, ), o el re#, (, afinado como un mi♭, ), podían sonar bastante mal, por lo que no convenía alejarse mucho de las tonalidades más cercanas a la escala natural. Podéis apreciarlo en la espiral logarítmica de la semana pasada.

Semitonos cromáticos y diatónicos

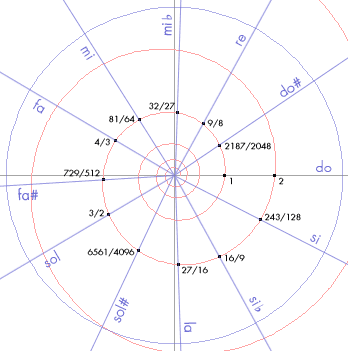
En este gráfico tenéis la misma espiral con las frecuencias de la escala cromática, pero esta vez, dado que cada 360º se repite el mismo sonido, he unido cada nota con el origen. Así, podemos ver todos los sonidos en una misma octava y observar más fácilmente los ángulos que las separan (representativos de los intervalos correspondientes). Aunque pueda parecerlo, los 12 ángulos de la imagen (12 semitonos), no son exactamente iguales: hay cinco de mayor tamaño (semitonos cromáticos) y 7 más pequeños (diatónicos).

Los semitonos cromáticos son los que hay entre notas con el mismo nombre, una natural y otra alterada, esto es, entre: do-do#, mi♭-mi, fa-fa#, sol-sol# y si♭-si. Todas estas notas se hayan en proporción de . En la imagen podéis apreciar que los ángulos son claramente mayores que los correspondientes a los semitonos diatónicos (semitonos entre notas con distinto nombre): do#-re, re-mi♭, mi-fa, fa#-sol, sol#-la, la-si♭ y si-do. La proporción en este caso es de . La diferencia, de nuevo, no es mucha: exactamente de una coma pitagórica:

Todo esto los violinistas lo saben bien, pues, a pesar de que este sistema de afinación ya no se utiliza, suele sonar mejor una nota sostenida (como fa#, sensible) que resuelve ascendentemente (sol), si ambos sonidos  están más próximos, como separados por un semitono diatónico. Por eso, quizás lleguéis a escucharles decir que las enarmonías no son posibles, que un sol♭ no es lo mismo que un fa# y demás, pero siempre en boca de la cuerda frotada: un pianista se partiría el culo.

Por último, podéis comprobar por qué la 5ª del lobo es más pequeña que el resto: mientras todas las demás tienen 3 semitonos cromáticos y 4 diatónicos, el intervalo entre mi♭ y sol#, tiene 2 semitonos cromáticos y 5 diatónicos. La diferencia es, por tanto, la prevista: una coma pitagórica.

Nota para músicos

Supongo que muchos ya habréis caído en la cuenta al leer estas entradas: el origen de la escala heptatónica explica también el orden de las tonalidades y de las alteraciones en la armadura de clave. Sol Mayor, por ejemplo, necesita solo un sostenido, pues al estar una 5ª por encima de do, utiliza los mismos intervalos para construir su escala y únicamente «se sale» de los sonidos naturales en la última 5ª,  de si a fa#.

Cada octava, en el sistema musical occidental, está dividida en 12 semitonos que juntos forman la escala cromática. Estos son los 12 sonidos básicos con los que está escrita el 90% de la música que conocemos y solemos escuchar, desde el medievo hasta nuestros días. El sistema no lo inventó pitágoras: surgió en Europa en la Baja Edad Media. Sin embargo, es consecuencia de la idea de afinar los intervalos por quintas, de ahí que sigamos hablando de afinación pitagórica. La división en 12 sonidos, por tanto, no es una cuestión trivial ni arbitraria: parte de una base previa, con sus ventajas e inconvenientes.

Muchos músicos a lo largo de toda la historia han propuesto sistemas diferentes, con una octava dividida en más sonidos. Prueba de ello son los teclados de instrumentos antiguos, muchos del Renacimiento (la época dorada de la música instrumental), que pueden llegar a tener hasta 31 teclas por octava (podéis encontrar más fotos aquí o pinchando sobre la imagen), o las teorías de músicos contemporáneos interesados en el microtonalismo (Rodion Romanov nos habló en un comentario de sonido 13, por ejemplo, donde proponen un sistema de 96 sonidos por octava, pero hay muchos más).

El círculo de 5^as

La semana pasada vimos que los sonidos de la escala natural se obtenían sumando quintas desde un sonido de partida dado (en nuestro ejemplo, el do). Si continuásemos haciéndolo hasta completar 12 quintas obtendríamos los 5 sonidos que nos faltaban: las notas alteradas (las teclas negras). Sin embargo: ¿por qué pararse en el sonido número 12? Bien, la respuesta es que al subir 12 quintas, volvemos a obtener el sonido original, solo que 7 octavas más arriba. El sonido original… más o menos, de hecho, más bien menos que más y es que, como imaginaréis, por más que multipliquemos 3/2 a la enésima potencia nunca obtendremos, exactamente, una potencia de 2 y por tanto, nunca volveremos a oír exactamente el sonido del que partimos. Por ello, con este tipo de afinación el círculo de quintas no es tal: nunca llega a cerrarse. Se parece más a una espiral que podríamos prolongar hasta el infinito, obteniendo siempre sonidos intermedios de los que ya tenemos. Y aquí es donde nace la discrepancia: la espiral, en efecto, puede forzarse para quedar cerrada en el sonido número 12. A fin de cuentas, el sonido número 13 se hallaría a relativamente poca distancia del punto de partida y nuestra capacidad de discernir es limitada. Pero esta solución no es la única, según muchos tampoco la mejor y desde luego, tiene sus desventajas. Para entender la polémica pasaremos a analizar lo imperfecto que, de hecho, es el «círculo de quintas».

12 quintas no son 7 octavas

No, no lo son. Podéis comprobarlo con una calculadora: . De hecho, la diferencia parece bastante significativa. Sin embargo, debemos recordar que en música las «distancias» se perciben como proporciones. Si realizamos esta operación, vemos que el resultado es bastante parecido a 1: . Este intervalo se conoce como coma pitagórica y es menos de un octavo de tono.

En esta gráfica podéis ver una espiral logarítmica donde la frecuencia de cada sonido viene representada: . De este modo, cada vez que el ángulo se hace ó , obtenemos una nueva potencia de 2, esto es, volvemos a oír un do.

En este tipo de gráfica los intervalos vienen dados por ángulos: a ángulos iguales, intervalos iguales. El intervalo de 8ª, vendría representado por un ángulo de 2π. Para calcular el ángulo correspondiente a otra frecuencia o intervalo, invertiremos la fórmula anterior: . Así podemos hallar también el ángulo correspondiente a una 5ª: . O el ángulo correspondiente a la coma pitagórica (esto es: la distancia entre el re# y el mi♭, o entre el si# y el do), bastante pequeño en comparación: .

Este pequeño error, no obstante, supone bastantes inconvenientes de cara al desarrollo posterior de la música tonal. Por ello, el sistema de afinación pitagórico terminó siendo rechazado en pro del sistema temperado que utilizamos actualmente. En la próxima entrada veremos cuáles son estos inconvenientes.